These lecture notes are my own notes that I made in order to use during the lecture, and it is approximately what I will be saying in the lecture. These notes may be brief, incomplete and hard to understand, not to mention in the wrong language, and they do not replace the lecture or the book, but there is no reason to keep them secret if someone wants to look at them.
Idag: Maskinoberoende optimering. Intermediärkod. Treadresskod.
Man menar egentligen inte "optimalt" (bästa möjliga), utan bara "bättre".
Det heter "optimization" på engelska, och "optimering" på svenska. Inte "optimisering"!
Normalt är det optimeringsfasen (-faserna) i kompilatorn som gör optimeringen, men det finns också "handoptimering", där programmeraren själv ändrar programmet. Ett exempel: i = i * 2 kan ändras till i = i << 2. Bitskiftning är en enklare operation än multiplikation, och kan på en del processorer vara snabbare.
Ett annat exempel:
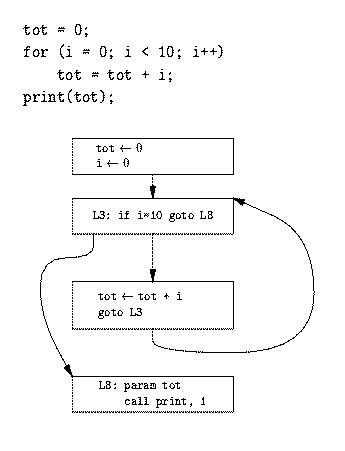
for (i = 0; i < n; ++i) {
do_something(a[i]);
}
Ekvivalent med:
i = 0;
while (i < n) {
do_something(a[i]);
++i;
}
Kan "optimeras" till att stega fram en pekare,
och använda den som loopvariabel:
p = &a[0];
p_after = &a[n];
while (p != p_after) {
do_something(*p);
++p;
}
Men moderna kompilatorer kan sånt här!
Det blir förmodligen inte snabbare,
kanske till och med långsammare,
och koden blir svårläst och skör.
Görs bättre av den automatiska optimeraren i kompilatorn!
Two rules about optimization by hand:
|
Types of optimization:
Machine-dependent optimization is sometimes done using Peep-hole optimization (ALSU-07 8.7, ASU-86 9.9): Simple transformations of the generated assembly (or machine) code. Ex:
| can be changed to |
|
"Intermediate code" på engelsa. "Mellankod" eller ibland "intermediärkod" på svenska.
Why generate intermediate code? Why not do everything "in the Yacc grammar"? Some reasons:
Some ways to represent the program:
Men: Postfixkod är svårjobbat om man ska optimera.
Exempel på infixkod: 1*(a+2)*b
I ett syntaxträd är det ganska enkelt att hitta, och optimera bort, multiplikationen med 1.
(Görs i del B i
labb 7.)
Postfixkoden: 1 a 2 + * b *
Svårt att hitta multiplikationen med 1 i postfixkoden! Svårt att ta bort den!
Example: x + y * z
temp1 = y * z temp2 = x + temp2
Treadresskod har (högst) tre adresser i varje instruktion:
var1 = var2 operation var3
Note:
Treadresskod har högst tre adresser i varje instruktion. Fler typer:
var1 = operation var2
goto addr1
if var1 <= var2 goto addr3
Idea: Each internal node corresponds to a temp-variable!
Example: a = b * -c + b * -c (The tree in ASU-86 fig. 8.4a)
temp1 = - c temp2 = b * temp1 temp3 = - c temp4 = b * temp1 temp5 = temp2 + temp3 a = temp5
param temp4 param a param b call f, 3
Synthesized attributes:
E.addr = the name of the temporary variable
(kallades place i ASU-86)
E.code = the sequence of three-address statements that calculates the value
(or they could be written to a file instead of stored in the attribute)
| Production | Semantic rule |
|---|---|
| Start -> id = Expr | Start.code = Expr.code + [ id.addr ":=" Expr.addr ] |
| Expr -> Expr1 + Expr2 | Expr.addr = make_new_temp();
Expr.code = Expr1.code + Expr2.code + [ Expr.addr = Expr1.addr "+" Expr2.addr; ] |
| Expr -> Expr1 * Expr2 | Expr.addr = make_new_temp();
Expr.code = Expr1.code + Expr2.code + [ Expr.addr = Expr1.addr "*" Expr2.addr; ] |
| Expr -> - Expr1 | Expr.addr = make_new_temp();
Expr.code = Expr1.code + [ Expr.addr = "-" Expr1.addr; ] |
| Expr -> ( Expr1 ) | Expr.addr = Expr1.addr; // No new temp!
Expr.code = Expr1.code; |
| Expr -> id | Expr.addr = id.addr; // No temp!
Expr.code = ' '; // No code! |
(Se tabellen i ALSU-07 fig. 6.19, eller i ASU-86 fig. 8.15.)
While statement (very similar to generating stack machine code, see föreläsning 9):
| Production | Semantic rule |
|---|---|
| Stmt -> while ( Expr ) Stmt1 |
Stmt.before = make_new_label();
Stmt.after = make_new_label(); Stmt.code = [ "label" Stmt.before ] + Expr.code + [ "if" Expr.addr "==" "0" "goto" Stmt.after; ] + Stmt1.code + [ "goto" Stmt.before ] + [ "label" Stmt.after ]; |
(Se tabellen i ALSU-07 fig. 6.36, eller i ASU-86 fig. 8.23.)
| Op | Arg1 | Arg2 | result | |
|---|---|---|---|---|
| 0 | uminus | c | temp1 | |
| 1 | * | b | temp1 | temp2 |
| 2 | uminus | c | temp3 | |
| 3 | * | b | temp3 | temp4 |
| 4 | + | temp2 | temp4 | temp5 |
| 5 | := | temp5 | a |
Skip: Also "triples" (but they are hard to optimize) and "indirect triples" (as easy to optimize as quadruples, but more complicated).
"Basic blocks" används för optimering.
Ett par termer:

Fler termer:
Transformationer på basic blocks (kort, mer sen i exemplet):
| -> |
|
| -> |
|
| -> |
|
/* recursively sorts the array a, from a[m] to a[n] */
void quicksort(int m, int n) {
int i, j;
int v, x;
if (n <= m)
return;
i = m - 1; j = n; v = a[n];
while (1) {
do
i = i + 1;
while (a[i] < v);
do
j = j - 1;
while (a[j] > v);
if (i >= j)
break;
x = a[i]; a[i] = a[j]; a[j] = x; /* swap */
}
x = a[i]; a[i] = a[n]; a[n] = x; /* swap */
quicksort(m, j);
quicksort(i + 1, n);
}
Some optimizations are not possible on the source level.
Treadresskod för den fetmarkerade delen av quicksort-funktionen (ALSU fig. 9.2 eller ASU-86 fig. 10.4):
(1) i = m - 1 (16) t7 = 4 * i (2) j = n (17) t8 = 4 * j (3) t1 = 4 * n (18) t9 = a[t8] (4) v = a[t1] (19) a[t7] = t9 (5) i = i + 1 (20) t10 = 4 * j (6) t2 = 4 * i (21) a[t10] = x (7) t3 = a[t2] (22) goto (5) (8) if t3 < v goto (5) (23) t11= 4 * i (9) j = j - 1 (24) x = a[t11] (10) t4 = 4 * j (25) t12 = 4 * i (11) t5 = a[t4] (26) t13 = 4 * n (12) if t5 > v goto (9) (27) t14 = a[t13] (13) if i >= j goto (23) (28) a[t12] = t14 (14) t6 = 4 * i (29) t15 = 4 * n (15) x = a[t6] (30) a[t15] = x
Steps for the optimizer:
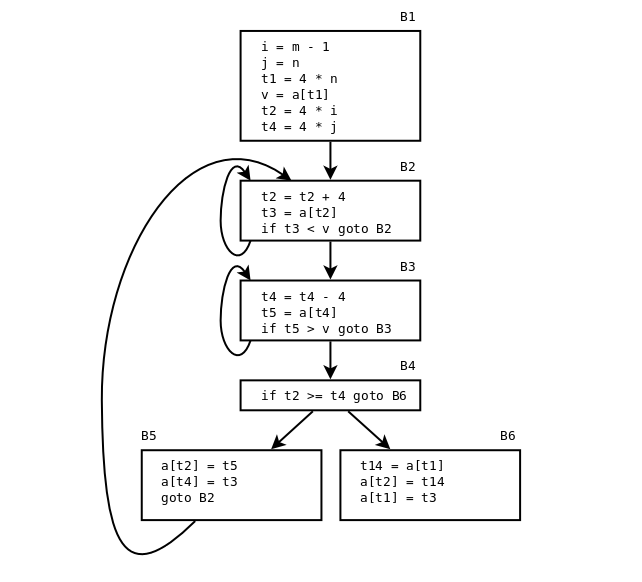
Basic blocks och flödesgraf för quicksort-funktionen (ALSU-07 fig. 9.3 eller ASU-86 fig. 10.5):
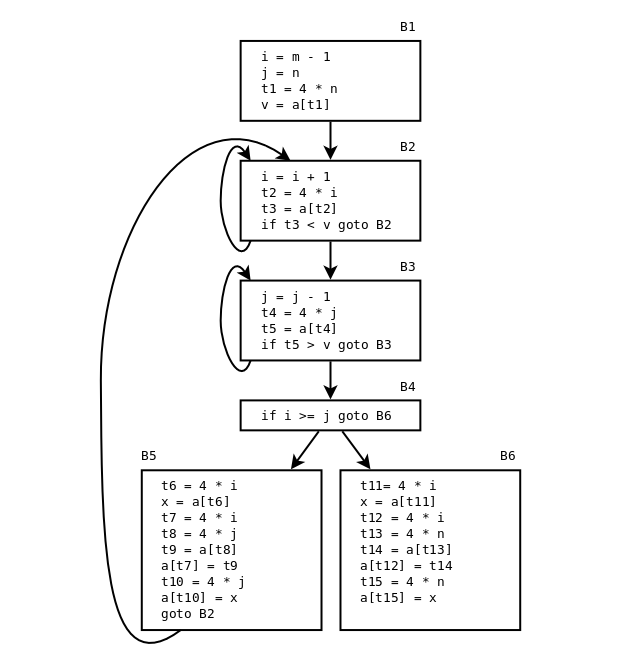
Three loops:
"Some of the most useful code-improving transformations".
Local transformation = inside a single basic block
Global transformation = several blocks (but inside a single procedure)
B5
| can be changed to |
B5
|
(Remove repeat calculations, use t6 instead of t7, t8 instead of t10.)
From ALSU-07 fig 9.4, 9.5:
(We can remove 4*i, 4*j, and 4*n completely from B6!)
Remove 4*i and 4*j completely from B5!
B5
| can be changed to |
B5
|
B5
| can then be changed to |
B5
|
Note: a hasn't changed, so a[t4] still in t5 from B3
B5
| can then be changed to |
B5
|
Blocken B5 och B6 efter att vi eleminerat både lokala och globala gemensamma deluttryck (ALSU-07 fig. 9.5 eller ASU-86 fig. 10.7):
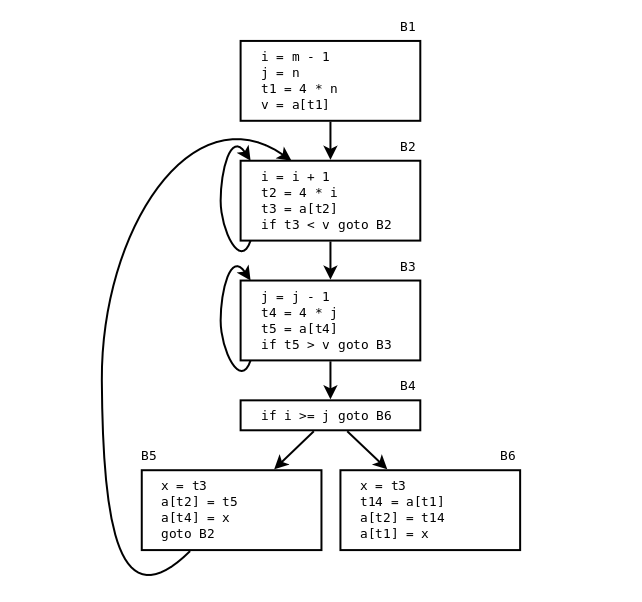
B5
| can be changed to |
B5
|
B5
| but x is dead, so: |
B5
|
while (i < limit - 2)
a[i++] = x + y;
The expressions limit - 2 and x + y are loop-invariant.
The next example is harder for the compiler, since strlen is just another function. (Or is it?)t1 = limit - 2; t2 = x + y; while (i < t1) a[i++] = t2;
for (i = 0; i < strlen(s1); ++i) s2[i] = s1[i];
n = strlen(s1); for (i = 0; i < n; ++i) s2[i] = s1[i];
i = 0;
j = 1;
while (a1[i] != 0) {
a2[j] = a1[i];
++i;
++j;
}
Both i and j are induction variables ("loop counters").
i = 0;
while (a1[i] != 0) {
a2[i + 1] = a1[i];
++i;
}
B3
| blir |
B3
|
Men det där är fel, för nu får t4 inget startvärde. Men det kan vi fixa genom att peta in t4 = 4*j i block B1, som körs en enda gång (inte i B2, som körs en massa massa gånger):
ALSU-07 fig. 9.9 (ASU-86 fig 10.9):
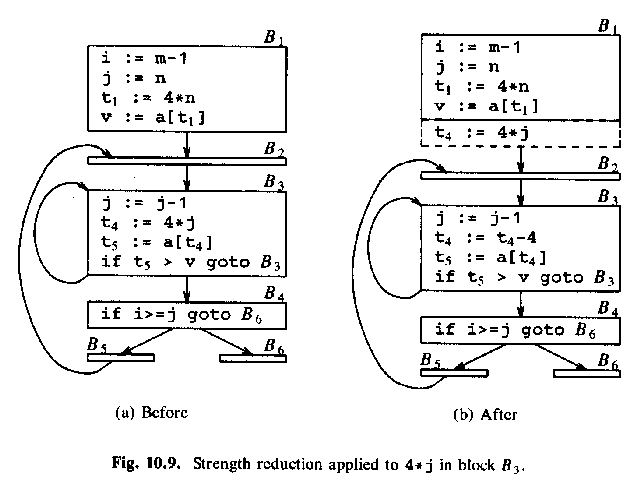
Then a similar strength reduction of 4 * i in basic block B2.
We know that t2 == 4 * i. Maintain this relationship!
Then, i and j are used only in the test int B4.
The test
i >= j
can be changed to
4 * t2 >= 4 * t4
(which is equivalent to
t2 >= t4).
i and j become dead!
Flödesgrafen efter att vi eliminerat induktionsvariablerna i och j (ASU-86 fig 10.10 eller ALSU-07 fig. 9.9):
for (i = 0; i < 20; ++i)
for (j = 0; j < 2; ++j)
a[i][j] = i + 2 * j;
may be transformed by unrolling the inner loop:
for (i = 0; i < 20; ++i) {
a[i][0] = i;
a[i][1] = i + 2;
}
or by unrolling the outer loop too:
a[0][0] = 0;
a[0][1] = 2;
a[1][0] = 1;
a[1][1] = 3;
a[2][0] = 2;
a[2][1] = 4;
....
a[19][0] = 19;
a[19][1] = 21;
Man behöver inte rulla ut alla varven, utan man kan rulla ut bara en del av dem.
Varning: cachen! En för stor loop kanske inte får plats i processorns instruktionscache.
void f(struct Node *p) {
if (p == NULL)
return;
p->value++;
f(p->next);
}
void f(struct Node *p) {
while (p == NULL) {
p->value++;
p = p->next;
}
}
int a;
...
void f(string a) {
...
while (1) {
int a;
... <-- In the debugger: print a
}
}
What is needed, for symbolic debugging in general?
A program may work when unoptimized, but not when optimized. For example, the C standard specifies undefined behaviour in certain cases. such as:
The behaviour depends entirely on what happens to be stored at the memory location 5 bytes after the end of s: unused padding, a variable, or the return address in an activation record? This can be different with or without optimization, since optimization, for example, can eliminate variables.char s[10]; ... s[14] = 'x';
An example program:
#include <stdlib.h> #include <stdio.h> int plus(int x, int y) { int a[2]; int s; s = x - y; a[x] = x + y; return s; } int main(void) { int resultat; resultat = plus(-1, -2); printf("resultat = %d\n", resultat); return 0; }
Running it without optimization, and then with optimization (the "-O" flag):
Excercise for the reader: What happened? Can you deduce something about how the compiler laid out the variables in the activation record for the function "plus"?
linux> gcc -Wall plus.c -o plus plus.c: In function 'plus': plus.c:5:9: warning: variable 'a' set but not used [-Wunused-but-set-variable] int a[2]; ^ linux> ./plus resultat = -3 linux> gcc -O -Wall plus.c -o plus plus.c: In function 'plus': plus.c:5:9: warning: variable 'a' set but not used [-Wunused-but-set-variable] int a[2]; ^ linux> ./plus resultat = 1 linux>
Trying to debug:
linux> gcc -g -O -Wall plus.c -o plus plus.c: In function 'plus': plus.c:5:9: warning: variable 'a' set but not used [-Wunused-but-set-variable] int a[2]; ^ linux> ./plus resultat = 1 linux> gdb plus Some output from GDB removed (gdb) break main Breakpoint 1 at 0x400562: file plus.c, line 12. (gdb) run Starting program: /home/padrone/tmp/14okt/plus Breakpoint 1, main () at plus.c:12 12 int main(void) { (gdb) step 15 printf("resultat = %d\n", resultat); (gdb) print resultat $1 = <optimized out> (gdb)
ASU-86 fig 10.68. Assume that the source, intermediate and target representation are the same.

ASU-86 fig 10.69. A DAG for the variables. The DAG shows how values depend on each other. Then, annotate it with life-time information.
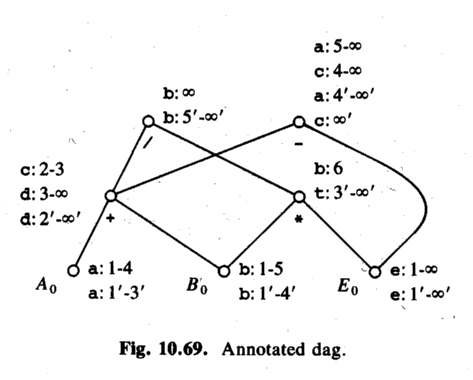
Example 1 (just the unoptimized program):
c = a + b after step 1. (Life time: 2-3)
c = c - e after step 3. (Life time: 4-infinity)
Example 2 (the optimized program):
c = a after step 5'. (Life time: 6'-infinty)
c is undefined in 1'-5'!
(But can be calculated, differently depending on when!)
Example 3:
An overflow occurs in the optimized code, in statement 2',
t = b * e.
The first source statement that uses the node b * e is 5.
Therefore, tell the user the program crashed in source statement 5!
Then the user says:
print b -> show b (lifetime 1-5 and 1'-4')
Explanation: b still has its initial value, both at 2' and at 5.
print c -> can't show actual stored c (lifetime 6-infinity)
Instead, find the DAG node for c at time 5 (-).
(Optimized) a will contain this value after 4', but not yet!
Consider the children:
d contains the value from the + node at 2'-infinity.
e contains the value from the E0 node at 1'-infinity.
So use d - e!
The course Compilers and interpreters | Lectures: 1 2 3 4 5 6 7 8 9 10 11 12