The course Compilers and interpreters | Lectures: 1 2 3 4 5 6 7 8 9 10 11 12
These lecture notes are my own notes that I made in order to use during the lecture, and it is approximately what I will be saying in the lecture. These notes may be brief, incomplete and hard to understand, not to mention in the wrong language, and they do not replace the lecture or the book, but there is no reason to keep them secret if someone wants to look at them.
Today: How to write a parser by hand
Example: Types in Pascal.
Examples:simple -> integer simple -> char simple -> num dotdot num type -> simple type -> ^ id type -> array [ simple ] of type
Example source program:integer 1..100 ^kundpost array [ integer ] of char array [ 20..40 ] of 0..3 array [ 1..5 ] of array [ 1..3 ] of 2..5
Tokens:
array [ num dotdot num ] of integer
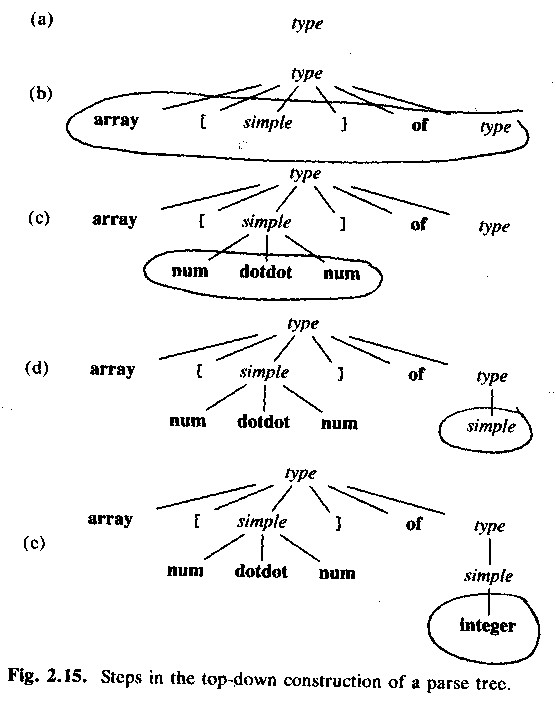
Top-down parsing, starting with a node for the non-terminal type.
Which of the productions (=rules) should we use? (Answer: type -> array ....)
Why? (Answer: The only production that starts with array.)
"Lookahead symbol" = "current token" = Sw: "aktuell token"
ASU-86 fig 2.15:

ASU-86 fig 2.16:
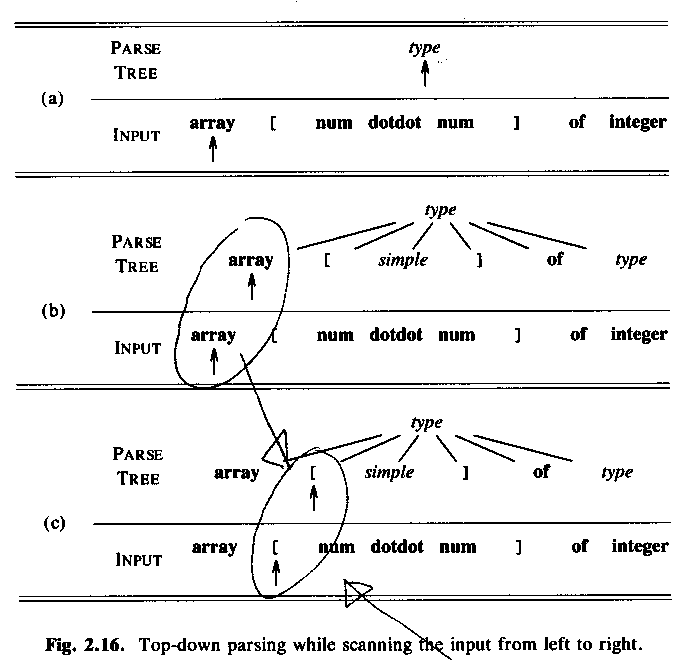
If always just one production possible to chose: predictive parsing, no backtracking
Recursive-descent parsing = the parser is a program with a procedure (in C: "function") for each non-terminal.
void simple() {
if (lookahead == integer)
match(integer);
else if (lookahead == char)
match(char);
else if (lookahead == num) {
match(num); match(dotdot); match(num);
}
else
error();
}
match() checks that the lookahead symbol (=current token) is the expected one,
and gets the next token (by calling the lexical analyzer).
When we write the function type(), it is not enough to see which tokens occur as the first token in the productions for type (^ and array). Since simple can occur as the first thing in a type, we must also see which tokens occur as the first token in productions for simple.
void type() {
if (lookahead == integer or lookahead == char or lookahead == num)
simple();
else if (lookahead == ^) {
match(^); match(id);
}
else if (lookahead == array) {
match(array); match([); simple(); match(]); match(of); type();
}
else
error();
}
FIRST(x) = all possible first tokens in strings that match x.
FIRST(simple) = the set { integer, id, char }
FIRST(^ id) = the set { ^ }
FIRST(array [ simple ] of type) = the set { array }
FIRST(type)
= the set { ^, array } + the set FIRST(simple)
= the set { ^, array, integer, id, char }
Recursive-descent without backtracking: if the grammar contains two rules...
...then FIRST(something) and FIRST(somethingelse) must be disjoint (=no common elements).NT -> something NT -> somethingelse
Use opt_stmts -> empty if nothing else matches opt_stmts, which will be when lookahead is end.stmt -> begin opt_stmts end opt_stmts -> stmt_list | empty
Implementation of a predictive, recursive-descent parser:expr -> expr + term
void expr() {
if (lookahead == num or lookahead == id)
expr();
else
...
Eliminate left recursion!
Rewrite this left-recursive production:
(A, x and y are just placeholders. A stands for some non-terminal, while x and y stand for sequences of both terminals and non-terminals. The book uses Greek letters: A -> A α | β)A -> A x | y
into these, which are not left-recursive:
(We can show that both these grammars describe the same language, namelt one y followed by zero, one or more x, by systematically expanding the starts ymbolen A in both grammars.)A -> y R R -> x R | empty
Example: rewrite this left-recursive production:
into these, which are not left-recursive:expr -> expr + term | term
A = exprexpr -> term rest rest -> + term rest | empty
First version: An expression is either a term, or you already have an expression (which may contain one or more terms) and we cteaye a new expression by adding a plus sign and a term.
Second version: An expression consists of a term, followed by a rest. This rest can either be empty (so the expression only consisted of that single term), or it consists of a plus sign and a term, followed by yet a rest (which may be empty or can contain one or more terms).
|
But note this!
The new, rewritten grammar contains different productions than the original did. Because of that, we'll obviously get a different parse tree for a particular expression! Among other things, the + operator has now become right associative instead of left associative! (Draw the different parse trees for term + term + term, if we prertend that term is a terminal.) But, as we will see in the next section: If you have a grammar with embedded semantic actions (that is, a so-called syntax-controlled translation scheme), if you include the semantic actions in the grammar transformations, they will be performed in the same order.) |
Ex: 2, 2+3, 2-3, 2-3+4+5-6
ASU-86 Fig 2.13/2.19 translation scheme for the program in 2.5:
expr -> expr + term { print('+') }
expr -> expr - term { print('-') }
expr -> term
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
Remember that term -> term + term was ambiguous
(Sw: tvetydig), so we transformed the grammar.
Rewrite the grammar to eliminate left recursion.
Important: Handle the semantic actions as part of the grammar,
when you rewrite it using the left-recursion elimination technique from above,
to get the prints done at the right places!
expr -> term rest
rest -> + term { print('+') } rest
rest -> - term { print('-') } rest
rest -> empty
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
The interesting parts of the program:
void term () {
if (isdigit(lookahead)) {
putchar(lookahead);
match(lookahead);
}
else
error();
}
void rest() {
if (lookahead == '+') {
match('+'); term(); putchar('+'); rest();
}
else if (lookahead == '-') {
match('-'); term(); putchar('-'); rest();
}
else
;
}
void expr() {
term(); rest();
}
Full source code: 2.5
| The rest is about Program 2.9. |
For example, when the source being read contains fnord, a call to lexan() will return 259 (which is the value ID, meaning that we have found an identifier), and put (for example) 16 in the variable tokenval, meaning that the identifier that was found is identifier number 16 in the symbol table.
Source code: lexer.c
Source code: symbol.c
Remember how stack macines work:
The course Compilers and interpreters | Lectures: 1 2 3 4 5 6 7 8 9 10 11 12