Lecture 6: Lexikalisk analys ("scanning"). Lex. Reguljära uttryck.

The course Compilers and interpreters | Lectures: 1 2 3 4 5 6 7 8 9 10 11 12

These lecture notes are my own notes that I made in order to use during the lecture, and it is approximately what I will be saying in the lecture. These notes may be brief, incomplete and hard to understand, not to mention in the wrong language, and they do not replace the lecture or the book, but there is no reason to keep them secret if someone wants to look at them.

Idag: Lexical analysis ("scanning"). Lex.

3 Lexical Analysis

3.1 The role of the lexical analyzer

Modularization of the compiler! Low module coupling!

3.2 Input buffering

Not so important.

3.3 Specification of tokens

Regular expressions

Important.

See also A Compact Guide to Lex & Yacc, click on Lex and then Practice.

Example 1: identifiers
letter ( letter | digit )*
Why not:
letter ( letter* | digit* )
Example 2: Unsigned numbers (17, 5.0, 6.23E-23)
digit -> 0 | 1 | 2 | ... | 9
digits -> digit digit*
optional_fraction -> . digits | empty
optional_exponent -> ( E ( + | - | empty ) digits ) | empty
num -> digits optional_fraction optional_exponent

Note! A grammar could have a rule digits -> digit digits but not a regular expression. Why not?

3.6 Finite automata

Just the beginning: ALSU-07 page 147-150 (ASU-86 page 113-117)

See also A Compact Guide to Lex & Yacc, click on Lex and then Theory.

Finite state automaton = finite state machine = finite automaton (in Swedish: ändlig tillståndsmaskin = ändlig tillståndsautomat = ändlig automat). A FSA can be in one of several states:

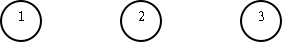
Three states for a FSA

It is called finite (Swedish: "ändlig") since it only has a finite (Swedish: ändligt) number of states.

We add some transitions, or edges (Sw: bågar) that lets the machine change state from one state to another:

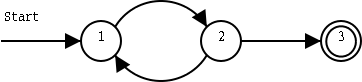
Three states, with transitions

In a deterministic finite state automaton, or DFA (Swedish: deterministisk tillståndsmaskin) transitions are determined by some sort of input:

DFA

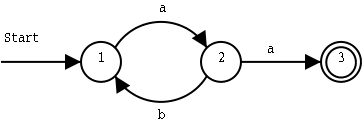
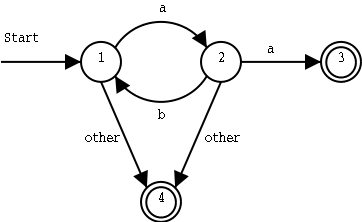
We move from state 1 to state 2 if we get an a as input. From state 2, we move back to state 1 if we get a b as input, and we move on to state 3 if we get an a.

To get from the start state to the end state, we must get an input string that starts with an a, and then has zero or more ba pairs. As soon as we get two a in a row, we move to the end state. These strings will work:

Regular expression:
a(ba)*a
If other input symbols than a and b can occur in the input, we should handle them too. We add a fourth state, which is also an end state, and were we will arrive as soon as we find anything else than a and b in the input:

Another DFA

A non-deterministic finite state automaton, or NFA (Swedish: icke-deterministisk tillståndsmaskin, icke-deterministisk automat), can have the same label on several transitions from a state. Try all of them at the same time. So a NFA can be in several different states at the same time!

Regular expressions easier to express with a NFA than with a DFA. A NFA can always be transformed to a DFA.

The NFA for (b|a)*ab (from KP page 37):

NFA

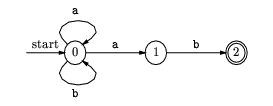
Can be transformed to:

DFA

Implementing a DFA

Several common ways:

3.4 Recognition of tokens

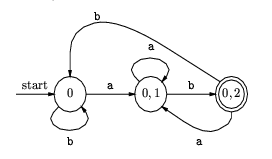
Again, the example with the format of an identifier:

letter ( letter | digit )*
Figure 2-1 from Niemann:

FSA

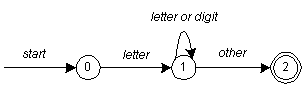
An implementation: 

start:  goto state0

state0: read c
        if c = letter goto state1
        goto state0

state1: read c
        if c = letter goto state1
        if c = digit goto state1
        goto state2

state2: accept string

3.5 A language for specifying lexical analyzers (Lex)

The context of Lex Lex (.l) input file format, similar to Yacc
%{
C declarations
%}
Lex definitions
%%
rules
%%
subroutines
Simple example, that just copies characters: 

%%
    /* match everything except newline */
.   ECHO;
    /* match newline */
\n  ECHO;

%%

int yywrap(void) {
    return 1;
}

int main(void) {
    yylex();
    return 0;
}

Another example: 

%{
  #include "yy.tab.h" // Def. of token codes: LT, LE, ELSE etc.
  extern int yylval;
%}

delim	[\t\n]
ws	{delim}+
letter	[A-Za-z]
digit	[0-9]
id	{letter}({letter}|{digit})*
num	{digit}+(\.{digit}+)?(E[+-]?{digit}+)?

%%

{ws}	{ /* no action and no return */ }
if	{ return IF; }
else	{ return ELSE; }
Else	{ return ELSE; }
[Ee][Ll][Ss][Ee]	{ return ELSE; }
{id}	{ yylval = install_id(yytext, yyleng);
          return ID; }
{num}	{ yylval = install_num(yytext, yyleng);
          return NUMBER; }
"<"	{ yylval = LT; return RELOP; }
"<="	{ yylval = LE; return RELOP; }
"="	{ yylval = EQ; return RELOP; }
"!="	{ yylval = NE; return RELOP; }
">"	{ yylval = GT; return RELOP; }
">="	{ yylval = GE; return RELOP; }

%%

int install_id(char* s, int n) {
  printf("Inserting into symbol table: '%s'\n", s);
  // ...
}

int install_num(char* s, int n) {
  double d;
  sscanf(s, "%lf", &d);
  printf("Found a number: %f\n", d);
  // ...
}

int yywrap() {
  printf("Calling yywrap...\n");
  return 1;
}

int main() {
  while (1)
    yylex();
  return 0;
}

Lex token spec for Niemann's calculator: 

%{
#include <stdlib.h>
#include "calc3.h"
#include "y.tab.h"
void yyerror(char *);
%}

%%

[a-z]       { 
                yylval.sIndex = *yytext - 'a';
                return VARIABLE;
            }

[0-9]+      {
                yylval.iValue = atoi(yytext);
                return INTEGER;
            }

[-()<>=+*/;{}.] {
                return *yytext;
             }

">="            return GE;
"<="            return LE;
"=="            return EQ;
"!="            return NE;
"while"         return WHILE;
"if"            return IF;
"else"          return ELSE;
"print"         return PRINT;

[ \t\n]+        ;       /* ignore whitespace */

.               yyerror("Unknown character");

%%

int yywrap(void) {
    return 1;
}

Pattern Matching Primitives in Lex (Table 2-1 from Niemann):

Metacharacter Matches
. any character except newline
\n newline
* zero or more copies of the preceding expression
+ one or more copies of the preceding expression
? zero or one copy of the preceding expression
^ beginning of line
$ end of line
a|b a or b
(ab)+ one or more copies of ab (grouping)
"a+b" literal a+b (C escapes still work)
\"a+b\" literal "a+b" (including the quote characters)
[] character class

Pattern Matching Examples from Lex (Table 2-2 from Niemann):

Expression Matches
abc abc
abc* ab abc abcc abccc ...
abc+ abc, abcc, abccc, abcccc, ...
a(bc)+ abc, abcbc, abcbcbc, ...
a(bc)? a, abc
[abc] one of: a, b, c
[a-z] any letter, a through z
[a\-z] one of: a, -, z
[-az] one of: - a z
[A-Za-z0-9]+ one or more alphanumeric characters
[ \t\n]+ whitespace
[^ab] anything except: a, b
[a^b] a, ^, b
[a|b] a, |, b
a|b a, b

(Moderna regexpar kan ha fler finesser.)

Lex variables and functions (Table 2-3 from Niemann):

Name Function
int yylex(void) call to invoke lexer, returns token
char *yytext pointer to matched string
yyleng length of matched string
yylval value associated with token
int yywrap(void) wrapup, return 1 if done, 0 if not done
FILE *yyout output file
FILE *yyin input file
INITIAL initial start condition
BEGIN condition switch start condition
ECHO write matched string

Reserved Words

(From Niemann.)

If your program has a large collection of reserved words, it is more efficient to let lex simply match a string, and determine in your own code whether it is a variable or reserved word. For example, instead of coding 

"if"            return IF;
"then"          return THEN;
"else"          return ELSE;

{letter}({letter}|{digit})*  {
         yylval.id = symLookup(yytext);
         return IDENTIFIER;
     }
where symLookup returns an index into the symbol table, it is better to detect reserved words and identifiers simultaneously, as follows: 
{letter}({letter}|{digit})*  {
         int i;

         if ((i = resWord(yytext)) != 0)
             return (i);
         yylval.id = symLookup(yytext);
         return (IDENTIFIER);
     }
This technique significantly reduces the number of states required, and results in smaller scanner tables.

The course Compilers and interpreters | Lectures: 1 2 3 4 5 6 7 8 9 10 11 12

Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se), August 29, 2022