Programmeringsmetodik: Vi lär oss det där med data: Grunderna om komplexitet

Exempel 1: Hus

Den här hundkojan är 1 meter hög, 1 meter bred och 1 meter djup.	Den här lagerlokalen är (tänker vi oss) 10 meter x 10 meter x 10 meter.	Vehicle Assembly Building, där NASA monterar ihop rymdraketer, är (tänker vi oss) 100 meter x 100 meter x 100 meter.

Alltså:

• Hundkojan är 1x1x1 meter,
• Lagerlokalen är 10x10x10 meter,
• VAB är 100x100x100 meter.

Hur lång tid tar det att att plantera blommor runt ytterväggen?

Lagerlokalen är ju 10 gånger större än hundkojan, med ytterväggar som är 10 gånger längre, och då tar det, kan vi gissa, 10 gånger längre tid att plantera blommor. VAB är 100 gånger större än hundkojan, med ytterväggar som är 100 gånger längre, och då tar det, kan vi gissa, 100 gånger längre tid att plantera blommor.

Det här är vad vi kallar linjär tidskomplexitet, eller som man brukar skriva, O(n) (uttalas ordo-n):

• Om problemet som ska lösas (i vårt fall huset som ska få blomrabatter) blir dubbelt så stort, så blir det dubbelt så mycket arbete att göra, och det tar dubbelt så lång tid.
• Om problemet som ska lösas blir tio gånger så stort, så blir det tio gånger så mycket arbete att göra, och det tar tio gånger så lång tid.
• Om problemet som ska lösas blir hundra gånger så stort, så blir det hundra gånger så mycket arbete att göra, och det tar hundra gånger så lång tid.
• Om problemet som ska lösas blir x gånger så stort, så blir det x gånger så mycket arbete att göra, och det tar x gånger så lång tid.

Hur lång tid tar det att att måla golvet?

Lagerlokalen är 10 gånger större än hundkojan, men ytan på golvet är 10*10 gånger större. Därför tar det, kan vi gissa, 10*10, dvs 100 gånger längre tid att måla golvet. VAB är 100 gånger större än hundkojan, med ett golv som har 100*100 gånger större yta, och då tar det, kan vi gissa, 100*100, dvs 10000 gånger längre tid att måla golvet.

Det här är vad vi kallar kvadratisk tidskomplexitet, eller som man brukar skriva, O(n²) (uttalas ordo-n-2):

• Om problemet som ska lösas blir dubbelt så stort, så blir det fyra gånger så mycket arbete att göra, och det tar fyra gånger så lång tid.
• Om problemet som ska lösas blir tio gånger så stort, så blir det hundra gånger så mycket arbete att göra, och det tar hundra gånger så lång tid.
• Om problemet som ska lösas blir x gånger så stort, så blir det x² gånger så mycket arbete att göra, och det tar x² gånger så lång tid.

Hur lång tid tar det att fylla huset med pingisbollar?

Lagerlokalen är 10 gånger större än hundkojan, men volymen inuti är 10*10*10 gånger större. Därför tar det, kan vi gissa, 1000 gånger längre tid att fylla upp den. VAB är 100 gånger större än hundkojan, med en innervolym som är 100*100*100 gånger större. Därför tar det, kan vi gissa, en miljon gånger längre tid att fylla upp den.

Det här är vad vi kan kalla kubisk tidskomplexitet, eller som man brukar skriva, O(n³) (uttalas ordo-n-3):

• Om problemet som ska lösas blir dubbelt så stort, så blir det åtta gånger så mycket arbete att göra, och det tar åtta gånger så lång tid.
• Om problemet som ska lösas blir tio gånger så stort, så blir det tusen gånger så mycket arbete att göra, och det tar tusen gånger så lång tid.
• Om problemet som ska lösas blir x gånger så stort, så blir det x³ gånger så mycket arbete att göra, och det tar x³ gånger så lång tid.

Hur lång tid tar det att att ta ett kort av huset?

Det här är vad vi kallar konstant tid, eller som man brukar skriva, O(1) (uttalas ordo-1):

Skilj på tid och tidskomplexitet!

Vi kan kalla den riktiga tiden (som man mäter med en klocka) för att utföra en uppgift för Tid(n). Till exempel kan Tid(n) för en viss uppgift vara 3n sekunder, så att med n=1 tar det 3 sekunder, med n=2 tar det 6 sekunder, med n=10 tar det 30 sekunder, och så vidare. Men tidskomplexiteten är fortfarande linjär, och skrivs O(n), inte O(3n).

Vi kommer att förklara mer längre ner om hur olika riktiga tider kan översättas till tidskomplexitet.

Exempel 2: Ballonger

En liten ballong.	En stor ballong.

• Tiden det tar att blåsa upp en ballong: O(n³)
• Tiden det tar att måla ballongen: O(n²)
• Tiden det tar att titta på ballongen: O(1)

• En ballong med diametern 2 dm tar 8 minuter att blåsa upp, 4 minuter att måla och 2 sekunder att titta på.
• En ballong med diametern 10 dm tar 1000 minuter att blåsa upp, 100 minuter att måla och 2 sekunder att titta på.
• En ballong med diametern 10 m tar en miljon minuter (ungefär två år) att blåsa upp, 1000 minuter att måla och 2 sekunder att titta på.

Gör det någon skillnad egentligen?

• Den svarta linjen visar ett program som alltid tar tiden 17, och som alltså har konstant tidskomplexitet: O(1)
• Den röda linjen visar ett program som tar tiden x för att hantera x stycken data, och som alltså har linjär tidskomplexitet: O(n)
• Den blå kurvan visar ett program som tar tiden x² för att hantera x stycken data, och som alltså har kvadratisk tidskomplexitet: O(x²)

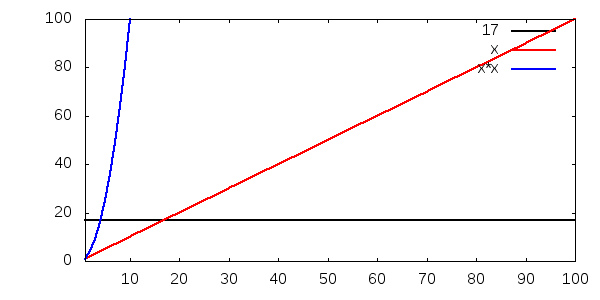
Sen visar vi samma bild igen, men med en annan skala på y-axeln. Notera hur både O(1) och O(n) knappt verkar stiga alls, jämfört med O(n²):

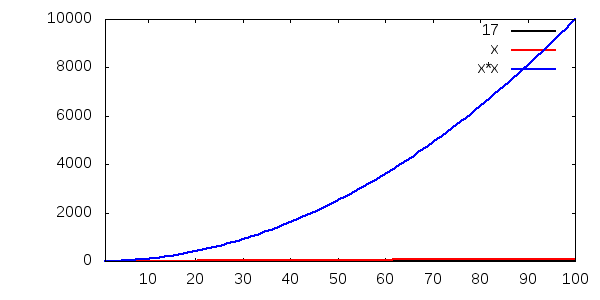
Ett annat sätt att visa hur snabbt O(n²) ökar, jämfört med O(1) och O(n), är den här tabellen, som visar (avrundade) tider, om vi antar att formlerna anger sekunder körtid:

Vi ser alltså att när mängden data växer, så kan skillnaderna i körtid bli stora mellan program med olika tidskomplexitet. En körning med en miljon indata tar alltså 12 dygn med det här O(n)-programmet, vilket man kanske kan stå ut med för en stor och viktig datakörning, till exempel en vetenskaplig simulering, men det är nog inte många som vill vänta i 30000 år på O(n²)-programmet.

Man struntar i konstanter

Vi kan ibland ange en formel för den riktiga tiden, i sekunder, för att lösa ett problem. Men denna riktiga tid är inte samma sak som tidskomplexiteten. Vi kan ta några exempel:

Därmed inte sagt att konstanterna aldrig är viktiga. En faktor 100 i körtid mellan två algoritmer kan mycket väl vara skillnaden mellan ett bra och ett oanvändbart program. Men det har inte med tidskomplexitet att göra.

Man bryr sig bara om den "dominerande termen"

När problemen är "små", dvs n är litet, så spelar algoritmens tidskomplexitet oftast inte så stor roll. Det är först när problemen blir stora, dvs n är stort, som det blir viktigt. Till exempel kanske en sorteringsalgoritm med tidskomplexiteten O(n³) fungerar jättebra för upp till något hundratal element som man ska sortera, men den blir olidligt långsam med 1000 element, och den tar flera veckor att köra med 10000. Med en miljon element tar den tusentals år.

Därför koncentrerar man sig på stora n när man håller på med tidskomplexitet. Och då kommer termerna med högre exponent att dominera. Säg till exempel att den verkliga tiden, i sekunder, för en algoritm anges av formeln:

Tid(n) = n³ + n² + n + 1

Med små n måste man räkna med alla fyra termerna (n³, n², n och 1), men ju större n blir, desto mer dominerar n³. Redan vid n = 10 står n³ för 90 procent av resultatet:

Därför struntar vi i alla termer utom den "dominerande", som (lite förenklat) är den med högst exponent. Exempel:

Därmed inte sagt att de andra termerna aldrig är viktiga. En konstantterm på en vecka, som kan ses som att det tar en vecka att överhuvudtaget köra igång programmet innan det börjar räkna, gör nog väldigt ofta programmet oanvändbart.

Några andra tidskomplexiteter

• Logaritmisk tidskomplexitet, t ex för binärsökning och sökning i träd: O(log n)
• En del sorteringsalgoritmer har O(n log n)
• Handelsresandeproblemet med fullständig sökning: O(n!)

Jämförelser

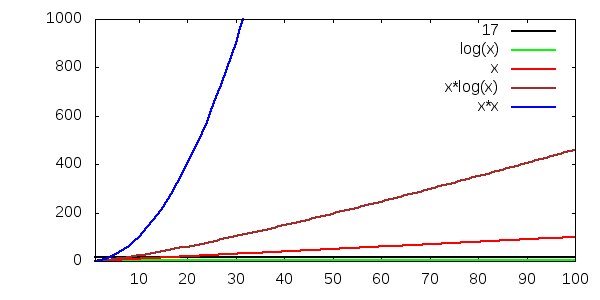
Till exempel ser vi att O(log n) är en "bra" tidskomplexitet, för den växer mycket långsamt.

Här har vi dessutom lagt till O(n³) och O(n!):

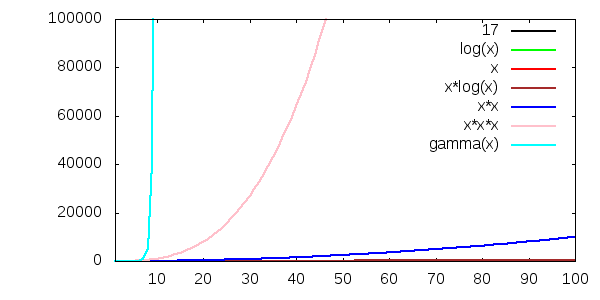
(Vi har använt gamma-funktionen för att plotta x!. Skalan är också annorlunda, så att de nya kurvorna ska få plats.)

n³ växer så snabbt att nu ser n² riktigt snäll ut. Och n! bara försvinner upp i skyn som en raket.

Några exempel med programkod

    int a[N];
    int summan = 0;
    for (int i = 0; i < N; ++i)
        summan += a[i];

    struct link* this_link = first_link;
    int summan = 0;
    while (this_link != NULL) {
        summan += this_link->talet;
        this_link = this_link->next;
    }

    int m[N][N];
    int summan = 0;
    for (int x = 0; x < N; ++x)
        for (int y = 0; y < N; ++y)
            summan += m[x][y];

    int m[N][N];
    int summan = 0;
    for (int x = 0; x < N; ++x)
        summan += m[x][x];

    int m[N][N];
    int summan = 0;
    for (int x = 0; x < N; ++x)
        summan += m[x][x];
    for (int x = 0; x < N; ++x)
        summan += m[x][N-x-1];

    int m[N][N][N];
    int summan = 0;
    for (int x = 0; x < N; ++x)
        for (int y = 0; y < N; ++y)
            for (int z = 0; z < N; ++z)
                summan += m[x][y][z];

Den här lösningen är O(n²), för funktionen strlen går igenom hela strängen och räknar antalet tecken, och det måste göras i loopvillkoret i varje varv i loopen, dvs vi går igenom hela strängen en gång för varje tecken i strängen:

    char* s = ......
    int antal = 0;
    for (int i = 0; i < strlen(s); ++i)
        if (s[i] == 'A')
            ++antal;

    char* s = ......
    int antal = 0;
    int n = strlen(s);
    for (int i = 0; i < n; ++i)
        if (s[i] == 'A')
            ++antal;

Läs mer

• Janlert et al, Datatyper och algoritmer, 2000: s 36-37 och kapitel 12, särskilt avsnitt 12.2
• Weiss, Data Structures and Algorithm Analysis in C++, 3d Ed, 2006: kapitel 2, särskilt avsnitt 12.1
• Svenska Wikipedia: Komplexitetsteori