Gäller som tentamen för:
DT2011 Datateknik B, Programmeringsmetodik, provkod 0100
DT2006 Datateknik B, Tillämpad datavetenskap B, provkod 0110
Ansvarig lärare är Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se), telefon 070-73 47 013.
Vi misstänker att det kan finnas fel i listan med avstånd, och nu ska vi skriva ett program som gör en rimlighetskontroll av avstånden i listan. Vi ska kolla att de angivna vägavstånden inte är kortare än avståndet fågelvägen.
På filen tatorter.txt finns data om alla svenska tätorter, 1956 stycken, med namn, vilken kommun de ligger i, folkmängd, SCB:s tätortskod, latitud, longitud och höjd över havet:
Värdet -9999 på en uppgift i filen betyder att den uppgiften saknas.
Det är alltså inte säkert att alla tätorterna har koordinater. Det är inte heller säkert att alla platserna i avståndstabellen finns med i listan med tätorter.
Jorden är rund, så om man vill räkna ut avståndet mellan två punkter på jordytan som man angett med latitud och longitud, räcker det inte med enkel plangeometri och Pythagoras sats. Men i närheten av Örebro kan man använda den här approximationen:
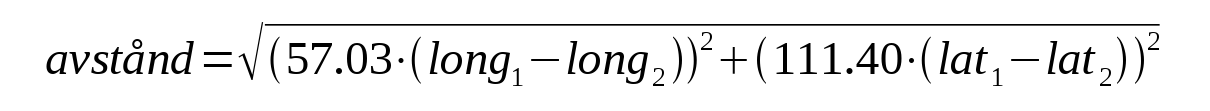
lat1 och long1 är den första punktens position, och lat2 och long2 den andras. Avståndet blir i kilometer.
Man kan använda dem om man vill, men måste inte.
| Lös denna uppgift först, och skicka in den. Spara också själv en kopia, ifall det blir något fel med posten! Börja inte med de andra uppgifterna innan du är klar med denna, och har skickat in den. |
Skriv ett program som går igenom listan med vägavstånd, och beräknar avståndet fågelvägen i de fall det går. Om detta beräknade fågelvägsavstånd är kortare än det angivna vägavståndet, är vägavståndet konstigt, och ett meddelande om det ska skrivas ut.
Exempel på hur en utskrift skulle kunna se ut:
Konstigt avstand: Arjeplog - Haparanda, 355 kilometer, är mindre än beräknade fågelvägen, 357.29 kilometer.
Alla upptäckta konstiga avstånd ska skrivas ut.
Det finns inga krav på några särskilda datastrukturer. Man kan använda arrayerna som finns med i filerna ovan, eller placera datat i egna datastrukturer. Om man gör egna datastrukturer ska det dock vara datastrukturer gjorda specifikt för detta ändamål, så använd inte någon generell datatyp som till exempel std::list. Man får, men behöver inte, dela upp programmet i flera filer.
| Lös först uppgift 1, och skicka in den. Därefter kan du lösa, och skicka in, den här uppgiften. Spara också själv en kopia, ifall det blir något fel med posten! Börja inte med uppgift 3 innan du är klar med denna, och har skickat in den. |
Programmet från uppgift 1 ovan fungerar bra, det går någorlunda snabbt att köra, och vi ska bara köra det en gång så prestanda spelar egentligen inte så stor roll. Men nu vill vi i alla fall snabba upp det.
Gör en datatstruktur för tätorterna där det går snabbt att hitta en ort med ett visst namn. Förslagsvis en hashtabell eller ett binärt träd. Använd sedan denna snabbare datastruktur för att slå upp tätorterna när avstånden ska kollas.
Datastrukturerna som används ska vara skapade specifikt för detta ändamål, så använd inte någon generell datatyp. Man får, men behöver inte, dela upp programmet i flera filer.
| Lös först uppgift 1 och 2, och skicka in dem. Därefter kan du lösa, och skicka in, den här uppgiften. Spara också själv en kopia, ifall det blir något fel med posten! |
Gör om uppgift 2 med hjälp av en generell datatyp.
Skapa först den generella datatypen (till exempel hashtabellen GenericHashTable). Välj själv metod för att skapa en generell datatyp. Dela upp på lämpliga filer. Det är inte förbjudet att inspireras av existerande lösningar, men du ska lämna in en som du gjort själv.
Använd den därefter i programmet.
| Den här sista-uppgiften för betyget 5 kanske kan ta lite längre tid att lösa. Om den inte är helt klar när tentatiden tar slut, är det därför tillåtet att skicka in en preliminär lösning, som man sedan kan komplettera. Ange tydligt att det är en preliminär lösning. Kompletteringen ska skickas in senast en vecka efter tentan. |