Gäller som tentamen för:
DT2011 Datateknik B, Programmeringsmetodik, provkod 0100
DT2006 Datateknik B, Tillämpad datavetenskap B, provkod 0110
Ansvarig lärare är Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se), telefon 070-73 47 013.
Tillägg: Lösningsförslag till uppgift 1 och 2

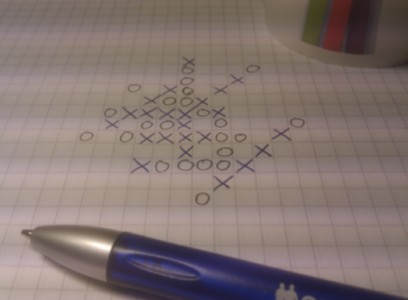
Vi håller på att skriva ett luffarschacksprogram, och som en del av det ska vi hantera "ställningar" eller "luffarschacksbräden", dvs en spelplan med ett antal kryss och ringar. På bilden ovan ser vi ett exempel.
Ett program som ska spela luffarschack på ett bra sätt måste hantera många sådana luffarschacksbräden: inte bara den aktuella ställningen på spelplanen, utan också ett stort antal olika möjliga framtida bräden, som programmet behöver utvärdera och välja mellan.
I luffarschack kan flera olika sekvenser av drag leda fram till samma bräde:
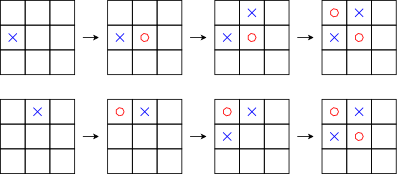
För att programmet ska slippa upprepa analyser och val av bräden som är likadana, är det bra om programmet kan jämföra bräden för att se om de är lika, och sen komma ihåg bara de unika brädena. Nu ska vi skriva och provköra den del av luffarschacksprogrammet som gör detta.
begin - - - - - - - - - - - - - x o - - - - - - x o x - - - - - - - o - - - - - - - - - - x o x - - - - - - x o - - - - - - - x o x - - - - - - - - o - - - - - - - - - - - - - - - - - - - - - - - - - - - - end |
Brädet är alltså 10 gånger 10 rutor stort, innehåller kryss (x), ringar (o) och tomma rutor (-), och avgränsas med orden begin och end.
En fil innehåller noll, ett eller flera bräden.
Skriv ett program som läser en sådan fil, och sedan talar om dels hur många bräden som fanns på filen, dels hur många av dem som var unika.
Programmet måste kunna hantera åtminstone 1000 unika bräden. Det finns inga krav på felhantering.
Programmet behöver lagra de unika bräden det hittar. Använd en array eller en länkad lista. Det ska vara datastrukturer gjorda specifikt för detta ändamål, så använd inte någon generell datatyp som till exempel std::list. Man får, men behöver inte, dela upp programmet i flera filer.
Exempelfiler som man kan provköra med:
| Lös först uppgift 1, och skicka in den. Därefter kan du lösa, och skicka in, den här uppgiften. Spara också själv en kopia, ifall det blir något fel med posten! Börja inte med uppgift 3 innan du är klar med denna, och har skickat in den. |
När ett luffarschacksprogram ska välja vilket drag det ska spela, genererar det och undersöker ett stort antal möjliga bräden. Det kan vara miljontals bräden.
Gör en ny version av programmet i uppgift 1, men med snabbare datastrukturer. Vi vill ha en enorm förbättring av prestanda.
Datastrukturerna som används ska vara skapade specifikt för detta ändamål, så använd inte någon generell datatyp. Man får, men behöver inte, dela upp programmet i flera filer.
Ytterligare en exempelfil som man kan provköra med om man vill:
| Lös först uppgift 1 och 2, och skicka in dem. Därefter kan du lösa, och skicka in, den här uppgiften. Spara också själv en kopia, ifall det blir något fel med posten! |
Gör om uppgift 2 med hjälp av en generell datatyp.
Skapa först den generella datatypen (till exempel hashtabellen GenericHashTable). Välj själv metod för att skapa en generell datatyp. Dela upp på lämpliga filer. Det är inte förbjudet att inspireras av existerande lösningar, men du ska lämna in en som du gjort själv.
Använd den därefter i programmet.
| Den här sista-uppgiften för betyget 5 kanske kan ta lite längre tid att lösa. Om den inte är helt klar när tentatiden tar slut, är det därför tillåtet att skicka in en preliminär lösning, som man sedan kan komplettera. Ange tydligt att det är en preliminär lösning. Kompletteringen ska skickas in senast en vecka efter tentan. |