Programmeringsmetodik: Vi lär oss det där med data: Grunderna om komplexitet

Tidskomplexitet handlar om hur lång tid det tar att köra ett program eller en algoritm. Men det handlar inte så mycket om ifall det tar 7 eller 8 sekunder, utan om hur tiden ändras när mängden data ändras. Om ett program ska sortera 1000 personer i skonummerordning, och det programmet tar 10 sekunder att köra, hur lång tid kommer det då att ta om vi i stället ska sortera 2000 personer? 10000? En miljon?

Exempel 1: Hus

För att illustrera tidskomplexitet ska vi börja med några exempel som inte handlar om programmering. Vi börjar med tre ganska kubformade hus:


Den här hundkojan är 1 meter hög, 1 meter bred och 1 meter djup.	Den här lagerlokalen är (tänker vi oss) 10 meter x 10 meter x 10 meter.	Vehicle Assembly Building, där NASA monterar ihop rymdraketer, är (tänker vi oss) 100 meter x 100 meter x 100 meter.

Alltså:

Hundkojan är 1x1x1 meter,
Lagerlokalen är 10x10x10 meter,
VAB är 100x100x100 meter.

Hur lång tid tar det att att plantera blommor runt ytterväggen?

Låt oss säga att det tar 1 timme att plantera blommor runt ytterväggen på hundkojan. Då tar det förmodligen 10 timmar att plantera blommor runt lagerlokalen, och 100 timmar runt VAB.

Lagerlokalen är ju 10 gånger större än hundkojan, med ytterväggar som är 10 gånger längre, och då tar det, kan vi gissa, 10 gånger längre tid att plantera blommor. VAB är 100 gånger större än hundkojan, med ytterväggar som är 100 gånger längre, och då tar det, kan vi gissa, 100 gånger längre tid att plantera blommor.

Det här är vad vi kallar linjär tidskomplexitet, eller som man brukar skriva, O(n) (uttalas ordo-n):

Om problemet som ska lösas (i vårt fall huset som ska få blomrabatter) blir dubbelt så stort, så blir det dubbelt så mycket arbete att göra, och det tar dubbelt så lång tid.
Om problemet som ska lösas blir tio gånger så stort, så blir det tio gånger så mycket arbete att göra, och det tar tio gånger så lång tid.
Om problemet som ska lösas blir hundra gånger så stort, så blir det hundra gånger så mycket arbete att göra, och det tar hundra gånger så lång tid.
Om problemet som ska lösas blir x gånger så stort, så blir det x gånger så mycket arbete att göra, och det tar x gånger så lång tid.

(Man skiljer egentligen på olika sorters tidskomplexitet: maxtid, genomsnittstid och minsta tid. Men det struntar vi i här. Och så finns det rumskomplexitet. Det struntar vi också i.)

Hur lång tid tar det att att måla golvet?

Låt oss säga att det tar 1 timme att måla golvet i hundkojan. Då tar det förmodligen 100 timmar att måla golvet i lagerlokalen, och 10000 timmar i VAB.

Lagerlokalen är 10 gånger större än hundkojan, men ytan på golvet är 10*10 gånger större. Därför tar det, kan vi gissa, 10*10, dvs 100 gånger längre tid att måla golvet. VAB är 100 gånger större än hundkojan, med ett golv som har 100*100 gånger större yta, och då tar det, kan vi gissa, 100*100, dvs 10000 gånger längre tid att måla golvet.

Det här är vad vi kallar kvadratisk tidskomplexitet, eller som man brukar skriva, O(n²) (uttalas ordo-n-2):

Om problemet som ska lösas blir dubbelt så stort, så blir det fyra gånger så mycket arbete att göra, och det tar fyra gånger så lång tid.
Om problemet som ska lösas blir tio gånger så stort, så blir det hundra gånger så mycket arbete att göra, och det tar hundra gånger så lång tid.
Om problemet som ska lösas blir x gånger så stort, så blir det x² gånger så mycket arbete att göra, och det tar x² gånger så lång tid.

Hur lång tid tar det att fylla huset med pingisbollar?

Låt oss säga att det tar 7 timmar att fylla hundkojan med pingisbollar. Då tar det förmodligen 7000 timmar att fylla lagerlokalen, och 7 miljoner timmar i VAB.

Lagerlokalen är 10 gånger större än hundkojan, men volymen inuti är 10*10*10 gånger större. Därför tar det, kan vi gissa, 1000 gånger längre tid att fylla upp den. VAB är 100 gånger större än hundkojan, med en innervolym som är 100*100*100 gånger större. Därför tar det, kan vi gissa, en miljon gånger längre tid att fylla upp den.

Det här är vad vi kan kalla kubisk tidskomplexitet, eller som man brukar skriva, O(n³) (uttalas ordo-n-3):

Om problemet som ska lösas blir dubbelt så stort, så blir det åtta gånger så mycket arbete att göra, och det tar åtta gånger så lång tid.
Om problemet som ska lösas blir tio gånger så stort, så blir det tusen gånger så mycket arbete att göra, och det tar tusen gånger så lång tid.
Om problemet som ska lösas blir x gånger så stort, så blir det x³ gånger så mycket arbete att göra, och det tar x³ gånger så lång tid.

Hur lång tid tar det att att ta ett kort av huset?

Det spelar ingen roll hur stort huset är, utan det tar alltid lika lång tid att sikta med kameran och ta kortet. (Låt oss säga 3 sekunder.)

Det här är vad vi kallar konstant tid, eller som man brukar skriva, O(1) (uttalas ordo-1):

Exempel 2: Ballonger


En liten ballong.	En stor ballong.

Tiden det tar att blåsa upp en ballong: O(n³)
Tiden det tar att måla ballongen: O(n²)
Tiden det tar att titta på ballongen: O(1)

En ballong med diametern 1 dm tar (tänker vi oss) 1 minut att blåsa upp, 1 minut att måla och 2 sekunder att titta på. Då kan vi räkna ut att:

En ballong med diametern 2 dm tar 8 minuter att blåsa upp, 4 minuter att måla och 2 sekunder att titta på.
En ballong med diametern 10 dm tar 1000 minuter att blåsa upp, 100 minuter att måla och 2 sekunder att titta på.
En ballong med diametern 10 m tar en miljon minuter att blåsa upp, 1000 minuter att måla och 2 sekunder att titta på.

Gör det någon skillnad egentligen?

Här har vi ritat upp ett diagram över hur lång tid tre olika program tar att köra.

Den svarta linjen visar ett program som alltid tar tiden 17, och som alltså har konstant tidskomplexitet: O(1)
Den röda linjen visar ett program som tar tiden x för att hantera x stycken data, och som alltså har linjär tidskomplexitet: O(n)
Den blå kurvan visar ett program som tar tiden x² för att hantera x stycken data, och som alltså har kvadratisk tidskomplexitet: O(x²)

Vi ser att den blå kurvan, med kvadratisk tidskomplexitet, sticker iväg väldigt snabbt mot mycket långa tider, medan den röda kurvan, med linjär tidskomplexitet, ökar mycket långsammare:

O(1), O(n) och O(n2)

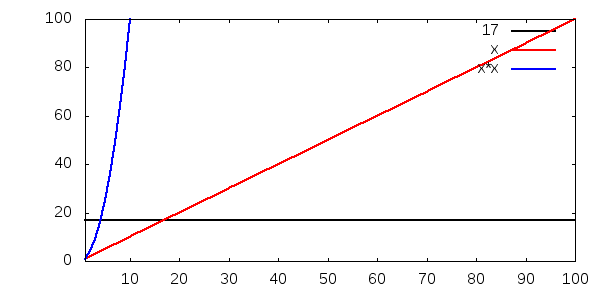
Sen visar vi samma bild igen, men med en annan skala på y-axeln. Notera hur både O(1) och O(n) knappt verkar stiga alls, jämfört med O(n²):

O(1), O(n) och O(n2)

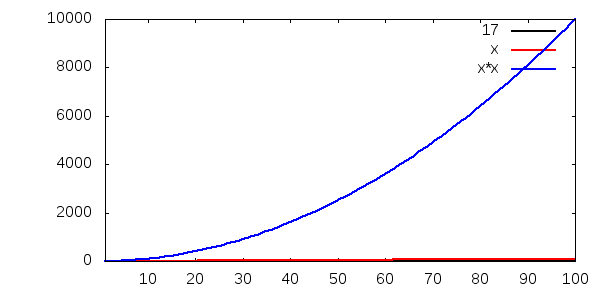
Ett annat sätt att visa hur snabbt O(n²) ökar, jämfört med O(1) och O(n), är den här tabellen, som visar (avrundade) tider, om vi antar att formlerna anger sekunder körtid:

Antal indata	O(1)-programmet	O(n)-programmet	O(n²)-programmet
1	17 sekunder	1 sekund	1 sekund
10	17 sekunder	10 sekunder	2 minuter
100	17 sekunder	2 minuter	3 timmar
1000	17 sekunder	17 minuter	12 dygn
1 miljon	17 sekunder	12 dygn	30000 år

Man struntar i konstanter

När problemet som vi ska lösa blir 100 gånger större, så är vi intresserade av hur mycket längre tid det tar. Tar det lika lång tid, 100 gånger längre tid, 10000 gånger längre tid, eller kanske en miljon gånger längre tid? Vi bryr oss inte så mycket om ifall det från början tog 3.7, 8.2 eller kanske 42 sekunder. Därför struntar vi i konstanter.

Vi kan ibland ange en formel för den riktiga tiden, i sekunder, för att lösa ett problem. Men denna riktiga tid är inte samma sak som tidskomplexiteten. Vi kan ta några exempel:

Riktig tid	Tidskomplexitet	Tidsökning om n blir 10 gånger större
Tid(n) = n	O(n)	10 gånger
Tid(n) = 1.02 n	O(n)	10 gånger
Tid(n) = 1000000 n	O(n)	10 gånger
Tid(n) = 0.00037 n	O(n)	10 gånger

Därmed inte sagt att konstanterna aldrig är viktiga. En faktor 100 i körtid mellan två algoritmer kan mycket väl vara skillnaden mellan ett bra och ett oanvändbart program. Men det har inte med tidskomplexitet att göra.

Man bryr sig bara om den "dominerande termen"

Den verkliga tiden för att köra en algoritm är ofta mer komplicerad än bara n² och n³. Man kanske måste ha med flera termer, som i n³ + n² + n. Men det gör inte så mycket, för när vi håller på med tidskomplexitet struntar vi i de "mindre" termerna (i det här fallet n² och n) och bryr oss bara om den största (n³).

När problemen är "små", dvs n är litet, så spelar algoritmens tidskomplexitet oftast inte så stor roll. Det är först när problemen blir stora, dvs n är stort, som det blir viktigt. Till exempel kanske en sorteringsalgoritm med tidskomplexiteten O(n³) fungerar jättebra för upp till något hundratal element som man ska sortera, men den blir olidligt långsam med 1000 element, och den tar flera veckor att köra med 10000. Med en miljon element tar den tusentals år.

Därför koncentrerar man sig på stora n när man håller på med tidskomplexitet. Och då kommer termerna med högre exponent att dominera. Säg till exempel att den verkliga tiden, i sekunder, för en algoritm anges av formeln:

Tid(n) = n³ + n² + n + 1

Med små n måste man räkna med alla fyra termerna (n³, n², n och 1), men ju större n blir, desto mer dominerar n³. Redan vid n = 10 står n³ för 90 procent av resultatet:

n	Tid(n)	Bara termen n³
1	4	1 (25%)
2	15	8 (53%)
3	40	27 (68%)
4	85	64 (75%)
10	1111	1000 (90%)
100	1010101	1000000 (99%)
1000	1001001001	1000000000 (99.9%)

Därför struntar vi i alla termer utom den "dominerande", som (lite förenklat) är den med högst exponent. Exempel:

Riktig tid	Tidskomplexitet	Tidsökning om n ökar från 1 miljon till 10 miljoner
Tid(n) = n + 1	O(n)	9.99999 gånger
Tid(n) = 17n + 1	O(n)	10 gånger
Tid(n) = 17n + 10000	O(n)	9.99471 gånger
Tid(n) = 0.01 n + 4711	O(n)	7.11 gånger
Tid(n) = n⁴ + 1000 n³ + 2000 n² + 33	O(n⁴)	9991 gånger

Därmed inte sagt att de andra termerna aldrig är viktiga. En konstantterm på en vecka, som kan ses som att det tar en vecka att överhuvudtaget köra igång programmet innan det börjar räkna, gör nog väldigt ofta programmet oanvändbart.

Kuriosa: Den naiva algoritmen för matrismultiplikation, dvs den som man får om man tittar efter i sin mattebok hur matrismultiplikation går till och sen skriver en sån funktion, har tidskomplexiteten O(n³). Men det finns andra algoritmer som med hjälp av olika trick kan snabba upp matrismultiplikationen. Den algoritm som har bäst tidskomplexitet är Coppersmith-Winograds algoritm, med en tidskomplexitet på O(n^2.376). Man skulle kunna tro att det betyder att den är snabbast. Tyvärr ingår det också en mycket stor konstantterm, som döljs av ordo-notationen, så Coppersmith-Winograds algoritm är tyvärr bara snabbast för matriser som är så stora att de inte kan hanteras med dagens datorer. (Källa: Engelska Wikipedias artiklar om matrismultiplikation och Coppersmith-Winograds algoritm.)

Några andra tidskomplexiteter

Logaritmisk tidskomplexitet, t ex för binärsökning: O(log n)
Många sorteringsalgoritmer har O(n log n)
Travelling salesman-problemet, fullständig sökning: O(n!)

Jämförelser

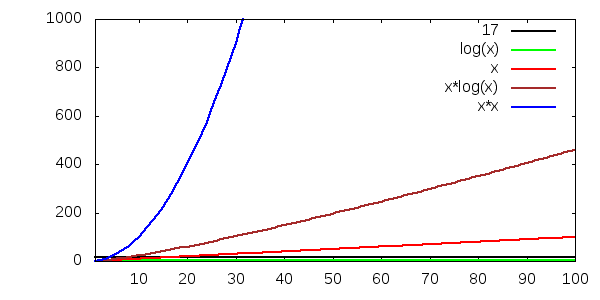
Här har vi några olika kurvor, som visar hur tiden växer med storleken på indata för fem program som är O(1), O(log n), O(n), O(n log n) och O(n²).

O(1), O(log n), O(n), O(n log n) och O(n2)

Till exempel ser vi att O(log n) är en "bra" tidskomplexitet, för den växer mycket långsamt.

Här har vi dessutom lagt till O(n³) och O(n!):

O(1), O(log n), O(n), O(n log n), O(n2), O(n3) och O(n!)

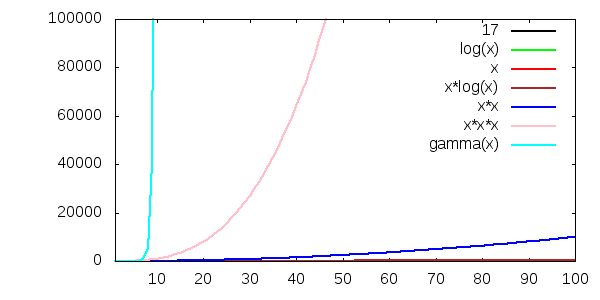
(Vi har använt gamma-funktionen för att plotta x!.)

n³ växer så snabbt att nu ser n² riktigt snäll ut. Och n! bara försvinner upp i skyn som en raket.

Några exempel med programkod

Summera talen i en array med längden n: O(n)

    int a[N];
    int summan = 0;
    for (int i = 0; i < N; ++i)
        summan += a[i];

Summera talen i en länkad lista med längden n: också O(n)

    struct link* this_link = first_link;
    int summan = 0;
    while (this_link != NULL) {
        summan += this_link->talet;
        this_link = this_link->next;
    }

Summera talen i en nxn-matris: O(n²)

    int m[N][N];
    int summan = 0;
    for (int x = 0; x < N; ++x)
        for (int y = 0; y < N; ++y)
            summan += m[x][y];

Summera diagonalen i samma nxn-matris: O(n)

    int m[N][N];
    int summan = 0;
    for (int x = 0; x < N; ++x)
        summan += m[x][x];

Summera talen i en tredimensionell nxnxn-matris: O(n³)

    int m[N][N][N];
    int summan = 0;
    for (int x = 0; x < N; ++x)
        for (int y = 0; y < N; ++y)
            for (int z = 0; z < N; ++z)
                summan += m[x][y][z];

Ofta kan man helt enkelt räkna antalet nästlade loopar. Men ibland kan man bli lurad. Anta till exempel att vi ska räkna antalet förekomster av bokstaven 'A' i en sträng med längden n.

Den här lösningen är O(n²), för funktionen strlen går igenom hela strängen och räknar antalet tecken, och det måste göras i loopvillkoret i varje varv i loopen, dvs vi går igenom hela strängen en gång för varje tecken i strängen:

    char* s = ......
    int antal = 0;
    for (int i = 0; i < strlen(s); ++i)
        if (s[i] == 'A')
            ++antal;

Den här lösningen däremot är O(n):

    char* s = ......
    int antal = 0;
    int n = strlen(s);
    for (int i = 0; i < n; ++i)
        if (s[i] == 'A')
            ++antal;

Läs mer

Janlert et al, Datatyper och algoritmer, 2000: s 36-37 och kapitel 12, särskilt avsnitt 12.2
Weiss, Data Structures and Algorithm Analysis in C++, 3d Ed, 2006: kapitel 2, särskilt avsnitt 12.1
Svenska Wikipedia: Komplexitetsteori

Thomas Padron-McCarthy (Thomas.Padron-McCarthy@oru.se), 14 september 2010