• Write clearly. Solutions that can't be read can of course not give any points. Unclear and ambiguous wording will be misinterpreted.
• Write the personal exam code on each sheet submitted. Do not write your name on the sheets.
• Write on only one side of the paper. Do not use a red pen.
• Assumptions beyond those in the given problems must be stated.
• You are allowed to explain your solutions. Even an incorrect answer may give some points, if the key ideas were right.

Formulas

1. Eliminating left recursion

A -> A x | y

The rule is replaced by the following two rules (or, more correctly, three productions), that describe the same language, but are not left recursive:

A -> y R
R -> x R | empty

2. Left factorization

A -> x y | x z

Replace with these three productions:

A -> x R
R -> y | z

Task 1 (6 p)

    a = b;
    if (c < d) {
        e = f * g / h + i + j;
    }
    else {
        if (k == l) {
            m = n;
        }
        else {
            o = p;
            q = r;
        }
        s = t / u / v;
        w = x;
    }

Translate the program segment to two of the following three types of representations.

a) an abstract syntax tree (by drawing it)

b) postfix code for a stack machine

c) three-address code

Note: Two of the three types, not all three. Should you answer with all three, the one with the highest points will be discarded.

Task 2 (3 p)

S -> S T | ε
T -> a U | a b U
U -> c

There are two problems with this grammar that makes it unsuitable for use by an LL(1) parser. That is the type of predictive top-down parser with one-token lookahead that we have seen for example in the 2.9 program. Explain the problems!

Task 3 (10 p)

a) activation record

b) basic block

c) loop unrolling

d) reference counting

Scenario for task 4-7

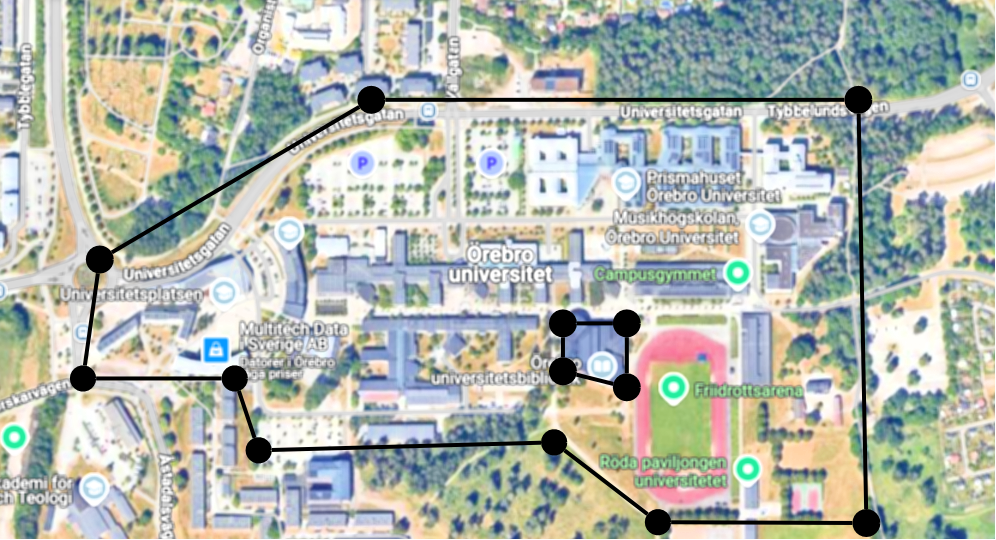
We want to use a special language to define the areas, like this:

map University {
    area Campus {
        corner 59.2562 N 15.2470 E
        corner 59.2562 N 15.2557 E
        corner 59.2519 N 15.2561 E
        corner 59.2524 N 15.2558 E
        corner 59.2525 N 15.2520 E
        corner 59.2532 N 15.2502 E
        corner 59.2536 N 15.2448 E
        corner 59.2537 N 15.2418 E
        corner 59.2548 N 15.2421 E
    }
    area Library {
        corner 59.2542 N 15.2504 E
        corner 59.2542 N 15.2515 E
        corner 59.2536 N 15.2515 E
        corner 59.2537 N 15.2505 E
    }
}

As we can see the input consists of a map, marked by the keyword map and the name of the map, followed by a list of one or more areas within curly brackets. The name is a single word that consists of English-alphabet letters.

An area is marked by the keyword area and a name, followed by a list of one or more corner points within curly brackets.

Finally a corner point is marked by the keyword corner and its map coordinates, first latitude and then longitude, each with a direction which can be N for north, E for east, W for west or S for south.

It should be possible to write the input in free format, so whitespace (blanks, tabs and newlines) should not be significant, except for separating the tokens.

Task 4 (4 p)

b) (2p) Out of these terminals, some will not have fixed lexemes. Write regular expressions for each such terminal.

Task 5 (5 p)

Task 6 (4 p)

map Kebnekaise {
    area Peak {
        corner 67.9187 N 18.5728 E
    }
}

Task 7 (8 p)