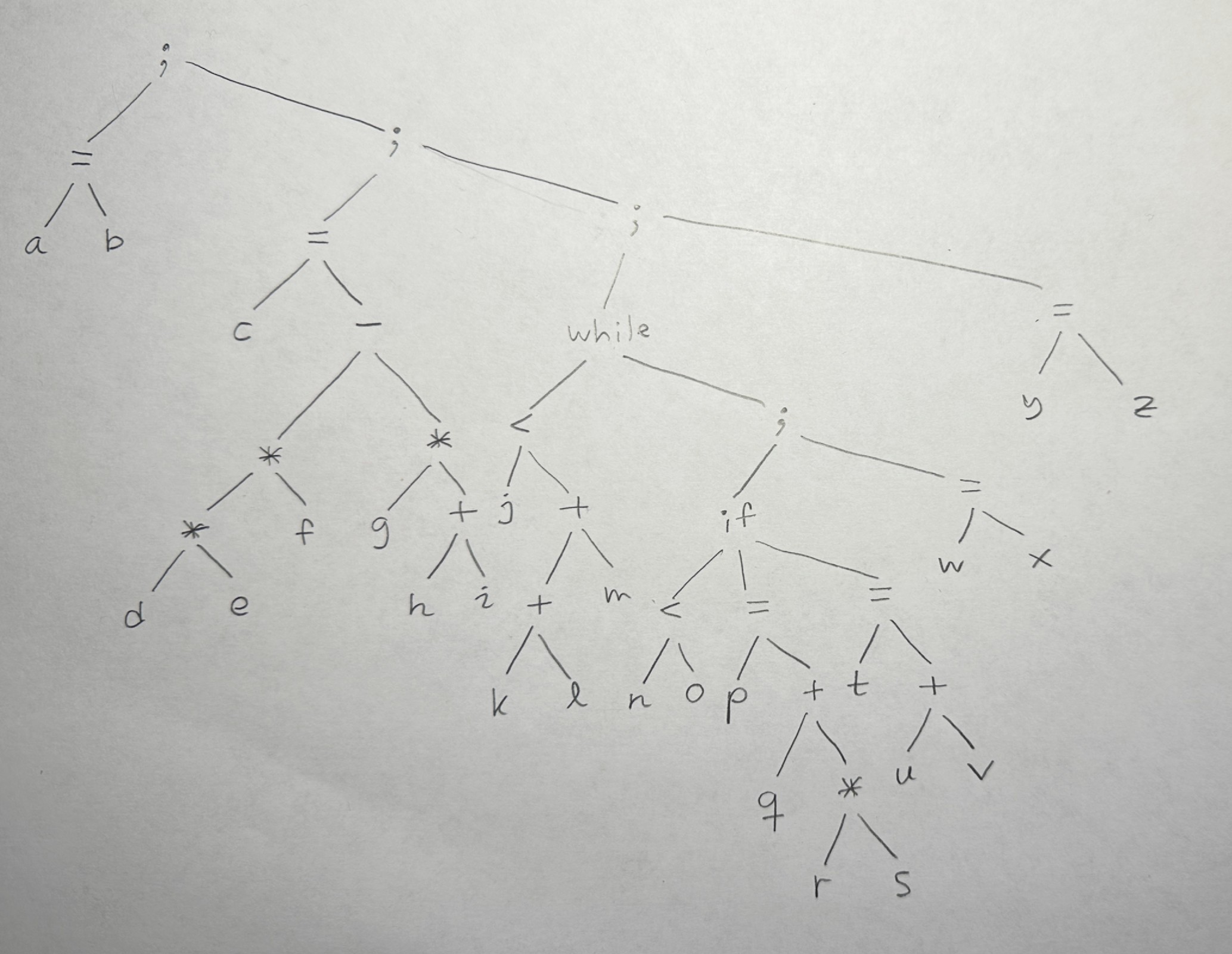
a = b;
c = d * e * f - g * (h + i);
while (j < k + l + m) {
if (n < o) {
p = q + r * s;
}
else {
t = u + v;
}
w = x;
}
y = z;
Translate the program segment to two of the following three types of representations. (Should you answer with all three, the one with the highest points will be discarded.)
a) an abstract syntax tree (by drawing it)
Answer:

b) postfix code for a stack machine
Answer:
lvalue a
rvalue b
=
lvalue c
rvalue d
rvalue e
*
rvalue f
*
rvalue g
rvalue h
rvalue i
+
*
-
=
label WHILE-START:
rvalue j
rvalue k
rvalue l
+
rvalue m
+
<
gofalse AFTER-WHILE
rvalue n
rvalue o
<
gofalse ELSE-START
lvalue p
rvalue q
rvalue r
rvalue s
*
+
=
goto AFTER-ELSE
label ELSE-START:
lvalue t
rvalue u
rvalue v
+
=
label AFTER-ELSE:
lvalue w
rvalue x
=
goto WHILE-START
label AFTER-WHILE:
lvalue y
rvalue z
=
c) three-address code
Answer:
a = b
t1 = d * e
t2 = t1 * f
t3 = h + i
t4 = g * t3
c = t2 - t4
label WHILE-START:
t5 = k + l
t6 = t5 + m
if j ≥ t6 goto AFTER-WHILE
if n ≥ o goto ELSE-START
t7 = r * s
p = q + t7
goto AFTER-ELSE
label ELSE-START:
t = u + v
label AFTER-ELSE:
w = x
goto WHILE-START
label AFTER-WHILE:
y = z
Or, if we number the instructions and use those numbers instead of labels:
(1) a = b (2) t1 = d * e (3) t2 = t1 * f (4) t3 = h + i (5) t4 = g * t3 (6) c = t2 - t4 (7) t5 = k + l (8) t6 = t5 + m (9) if j ≥ t6 goto 17 (10) if n ≥ o goto 14 (11) t7 = r * s (12) p = q + t7 (13) goto 15 (14) t = u + v (15) w = x (16) goto 7 (17) y = z
In which phase of the compiler, or at which other times, are the following errors detected?
| Program | Error |
|---|---|
a = b;
c = d * e * f - g * h + i);
while (j < k + l + m) {
while (n < o) {
p = q + r $ s;
}
else {
t = u + v;
}
w = x;
}
y = z;
|
variable "a" is set but not used unexpected end parenthesis unknown operator "$" "else" without a previous "if" variable "x" undeclared |
Answer:
We try to create a grammar for the language, with the following result. The start symbol is S, which represents a complete expression.
S -> S * T | T
T -> T ^ U | U
U -> U + number | number
a) Given this grammar, what is the precedence of the three operators?
Answer:
+ has the highest precedence, followed by ^, and * has the lowest-
b) Given this grammar, what is the associativity of the three operators?
Answer:
They are all left associative. For example, the expression 2+3+4 will be grouped as ((2+3)+4).
c) Using the normal rules for precedence and associativity,
the expression
12 + 13 * 14 ^ 15 * 16
would be interpreted as 12 + ((13 * (14 ^ 15)) * 16),
or, as a syntax tree:
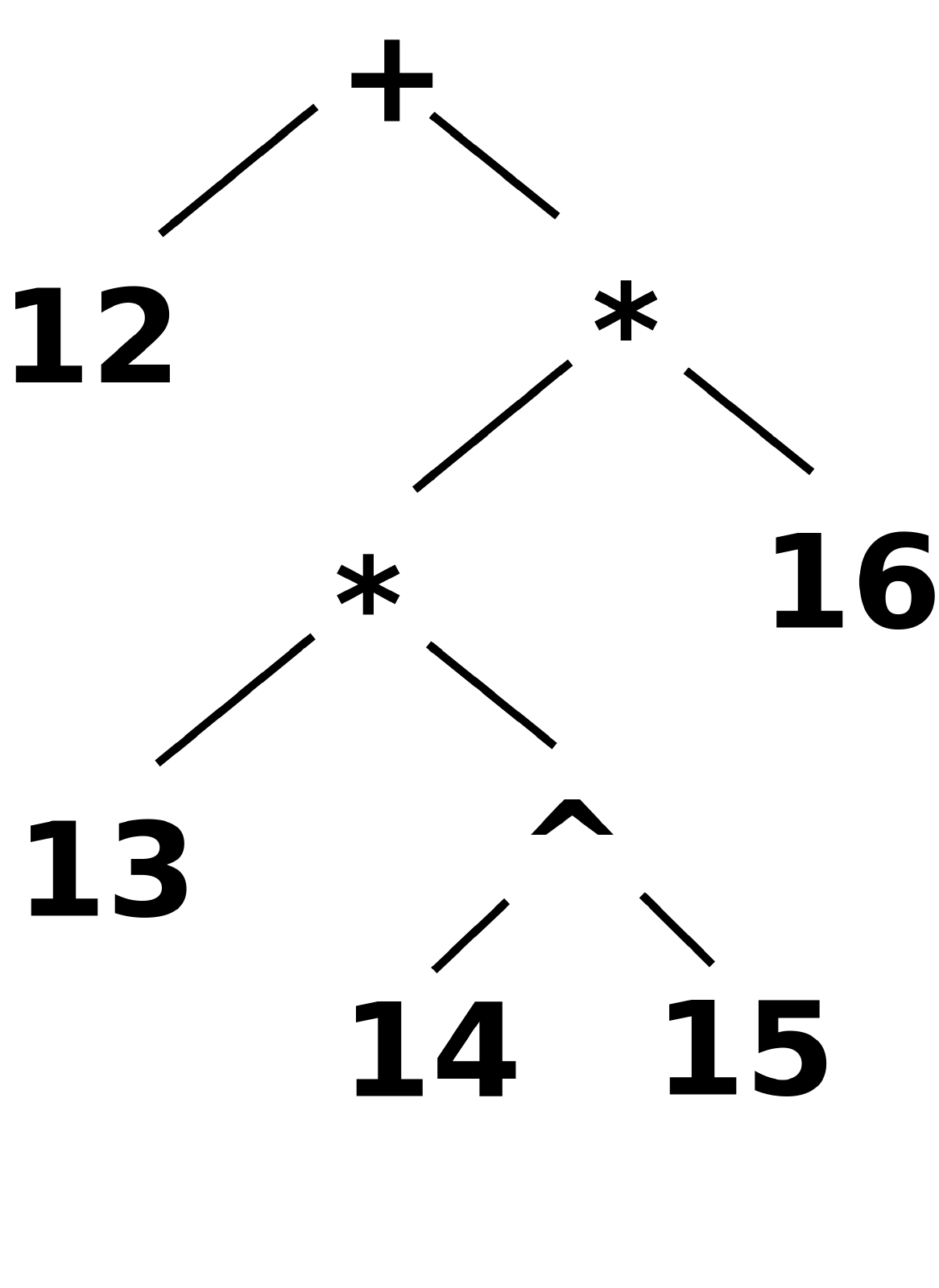
Draw the syntax tree for this expression when parsed using the grammar above!
Answer:
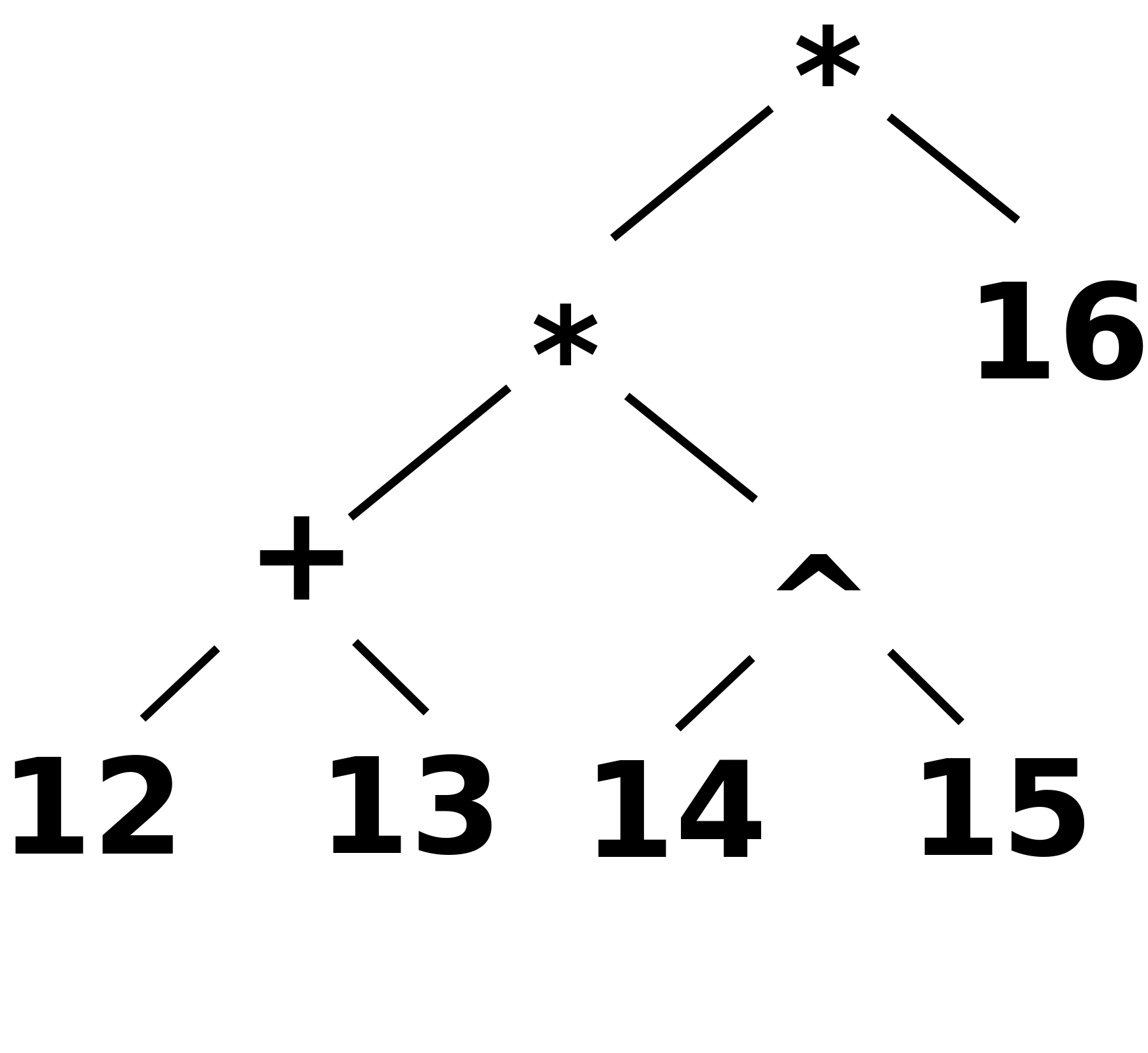
Written as an expression with parentheses: (((12 + 13) * (14 ^ 15)) * 16)

Unfortunately, for a while we have to wash our carpets a lot:


To keep track of our carpets, and when we have washed them, we design a program with a special input language. Here is an example of how this input language will look:
carpet 1 1.2; carpet 2 2; cleaned carpet 1 on 2023-10-23; carpet 3 0.6; cleaned carpet 2 on 2023-10-23; cleaned carpet 1 on 2023-10-24; carpet 4 1.2 * 2.0; carpet 5 1.2 * 5; done; |
As we can se, there are three commands that can be given: carpet, which defines a carpet with a number and an area, cleaned, which says that we have cleaned a certain carpet on a certain day, and done, which signals the end of the input.
The area of a carpet can be given as a single number, with or without decimals, or as a simple expression using the length and width of the carpet, as shown in the example above.
It should be possible to write the input in free format, so the following input should be equivalent to the one above:
carpet 1 1.2 ; carpet 2 2 ; cleaned carpet 1 on 2023-10-23 ; carpet 3 0.6 ; cleaned carpet 2 on 2023-10-23 ; cleaned carpet 1 on 2023-10-24 ; carpet 4 1.2 * 2.0 ; carpet 5 1.2 * 5 ; done ; |
Answer:
carpet
cleaned
on
done
semicolon (";")
times ("*")
date
integer (a number without decimals)
noninteger (a number with decimals)
b) (2p) Out of these terminals, some will not have fixed lexemes. Write regular expressions for each such terminal.
Answer:
date: [12][0-9][0-9][0-9]-[0-1][0-9]-[0-3][0-9]
integer: [0-9]+
noninteger: [0-9]+\.[0-9]+
Answer:
input -> commands donecommand
donecommand -> done semicolon
commands -> command commands | ε
command -> carpet integer area semicolon
| cleaned carpet integer on date semicolon
area -> number | number times number
number -> integer | noninteger
carpet 17 3.0; carpet 18 3 * 4; done; |
Answer:
Answer:
The grammar from the task above has a FIRST()-conflict, so we must first left factor the productions for the non-terminal area, which gives us this new grammar:
input -> commands donecommand
donecommand -> done semicolon
commands -> command commands | ε
command -> carpet integer area semicolon
| cleaned carpet integer on date semicolon
area -> number area-rest
area-rest -> times number | ε
number -> integer | noninteger
For testing, you can download carpetparser.c, plus a Lex scanner specification carpets.l, and a Bison version of the grammar carpets.y, and a Makefile.
int lookahead;
void match(int expected) {
if (lookahead != expected)
error();
else
lookahead = scan();
}
void input(void) {
commands(); donecommand();
}
void donecommand(void) {
match(DONE); match(SEMICOLON);
}
void commands(void) {
if (lookahead == CARPET || lookahead == CLEANED) {
command(); commands();
}
else {
/* Empty */
}
}
void command(void) {
if (lookahead == CARPET) {
match(CARPET); match(INTEGER); area(); match(SEMICOLON);
}
else if (lookahead == CLEANED) {
match(CLEANED); match(CARPET); match(INTEGER); match(ON); match(DATE); match(SEMICOLON);
}
else {
error();
}
}
void area(void) {
number(); area_rest();
}
void area_rest(void) {
if (lookahead == TIMES) {
match(TIMES); number();
}
else {
/* Empty */
}
}
void number(void) {
if (lookahead == INTEGER) {
match(INTEGER);
}
else if (lookahead == NONINTEGER) {
match(NONINTEGER);
}
else {
error();
}
}
void parse() {
lookahead = scan();
input();
printf("Ok.\n");
}
int main() {
printf("Write a complete input, ending with \"done\", a semicolon and EOF:\n");
parse();
}