| Observera: Det finns nio uppgifter på tentan. Välj ut och besvara (högst) åtta av dessa. (Skulle du svara på alla nio, räknas den med högst poäng bort.) |
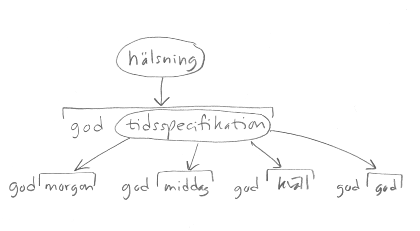
Språket består av följande fyra strängar:
Svaret kan man få fram genom att konstruera ett träd som utgår från startsymbolen hälsning, och sen rekursivt ersätta icke-terminaler med samtliga möjliga expansioner enligt produktionerna i grammatiken, tills alla lövnoder i trädet endast innehåller terminaler:

Rättningskommentar: 1 poäng för språket, 1 poäng för hur man gör. Att bara skriva "expandera till alla möjliga sekvenser av terminaler", utan att tala om hur det ska gå till, ger 0.5 poäng.
(b) (2p)
hälsningar -> minst-en-hälsning | empty minst-en-hälsning -> minst-en-hälsning ; hälsning | minst-en-hälsning
Den här grammatiken ger ett semikolon även efter den sista hälsningen:
hälsningar -> hälsning ; hälsningar | empty
Men den här grammatiken får man ett valfritt semikolon efter den sista hälsningen:
hälsningar -> hälsning ; hälsningar | hälsning | empty
Den här grammatiken ger alltid minst en hälsning, i stället för "noll, en eller flera", som det stod i uppgiften:
hälsningar -> hälsning ; hälsningar | hälsning
Den här grammatiken är tvetydig, och kan dessutom ge en massa extra semikolon:
hälsningar -> hälsningar ; hälsningar | hälsning | empty
Den här grammatiken funkar inte alls, för expansionen kan aldrig sluta:
hälsningar -> hälsningar ; hälsning
Rättningskommentar: Det står "åtskilda med semikolon", men inget poängavdrag om det alltid blir ett semikolon på slutet. -0.5 poäng för inga semikolon alls. -0.5 poäng för en eller flera i stället för noll, en eller flera. -1 poäng för en eller två stället för noll, en eller flera. -1 poäng för tvetydig grammatik.
(c) (1p)
En entydig grammatik är en grammatik där varje giltig sträng i språket har ett enda möjligt parse-träd. Exempelvis är den här grammatiken:
tvetydig, eftersom strängen a kan genereras med två olika träd:S -> a | T T -> a
S S
| |
a T
|
a
Rättningskommentar:
Högst 0.5 poäng om exempel saknas.
Parsern bygger upp ett parse-träd. Detta kan dock vara implicit, och kommer till uttryck bara genom i vilken ordning parsern går igenom reglerna i grammatiken när den matchar dem mot sekvensen av tokens från scannern.
Den semantiska analysen går igenom det parse-träd som parsern byggt upp (eller byggt upp implicit) och "dekorerar" det, till exempel med typinformation. Felmeddelanden om olika fel i källprogrammet, till exempel typfel, kan man också se som "utdata" från den semantiska analysen.
Utdata från mellankodsgeneratorn är, förstås, mellankod. Mellankoden kan bestå av treadresskod, men också något annat format, till exempel postfixkod eller ett syntaxträd.
Optimeraren bearbetar mellankoden på olika sätt, och utdata från den är alltså mellankod som flyttats om, och där vissa delar av mellankoden kanske kunnat tas bort.
positivt_tal [0-9]+
tal (-)?{positivt_tal}
heltalsspec \%{tal}?d
flyttalsspec \%{tal}?(.{positivt_tal})?f
strspec \%{tal}?(.{positivt_tal})?s
procentsak {heltalsspec}|{flyttalsspec}|{strspec}
vanligt_tecken [^\%]
sak {vanligt_tecken}|{procentsak}
format {sak}*
Eller om man vill vara mer kompakt:
d \%((-)?[0-9]+)?d
f \%((-)?[0-9]+)?(.[0-9]+)?f
s \%((-)?[0-9]+)?(.[0-9]+)?s
format ([^\%]|{d}|{f}|{s})*
Eller som ett enda klägg:
Rättningskommentar: -1 poäng om man har med "siffra" och "tecken" utan att ange regler för dem. -0.5 poäng om man helt struntat i fiskmåsklamrar (eller motsvarande).([^\%]|(\%((-)?[0-9]+)?d)|(\%((-)?[0-9]+)?(.[0-9]+)?f)|(\%((-)?[0-9]+)?(.[0-9]+)?s))*
Produktionen
är vänsterrekursiv, så den vänsterrekursionen måste elimineras. De två produktionernaT -> T U
har en FIRST()-konflikt, och måste vänsterfaktoriseras. Resultat av transformationerna:U -> c d U -> c d d
S -> a T | b T U T -> U R1 R1 -> U R1 | empty U -> c d R2 R2 -> d | empty
Rättningskommentar: Den här uppgiften visade sig vara lite svårare än jag hade tänkt, eftersom man egentligen måste vända på T och U i den andra produktionen för S, för att parsern ska fungera. Det uppstår nämligen en konflikt av en typ som vi inte tagit upp i kursen. Så här borde grammatiken bli:
S -> a T | b U T T -> U R1 R1 -> U R1 | empty U -> c d R2 R2 -> d | empty
b)
void error() {
printf("Ledsen error.\n");
exit(EXIT_FAILURE);
}
void match(int expected) {
if (lookahead != expected)
error();
else
lookahead = scan();
}
extern void S(), T(), U(), R1(), R2();
void S() {
printf("S\n");
if (lookahead == 'a') {
match('a'); T();
}
else if (lookahead == 'b') {
match('b'); U(); T(); /* Se rättningskommentaren ovan */
}
else
error();
}
void T() {
printf("T\n");
U(); R1();
}
void R1() {
printf("R1\n");
if (lookahead == 'c') {
U(); R1();
}
else {
/* Matchar empty, dvs nästa token kan vara vad som helst */
}
}
void U() {
printf("U\n");
match('c'); match('d'); R2();
}
void R2() {
printf("R2\n");
if (lookahead == 'd') {
match('d');
}
else {
/* Matchar empty, dvs nästa token kan vara vad som helst */
}
}
void parse() {
printf("parse\n");
lookahead = scan();
S();
match('$');
printf("Ok.\n");
}
Matchningen mot $, som vi antar markerar slutet på tokensekvensen i indata, behövs bara om det inte får komma mer data efter det som matchas av grammatiken. En del av felkontrollerna i programmet är redundanta. Spårutskrifterna, som skriver ut namnen på icke-terminaler, behöver förstås inte vara med.
sats -> for ( uttryck1 ; uttryck2 ; uttryck3 ) sats1
{
string före_testet = new_label();
string efter_loopen = new_label();
sats.kod =
uttryck1.kod +
instruktion(före_testet + ":") +
uttryck2.kod +
instruktion("if " + uttryck2.plats + " == 0 goto " + efter_loopen) +
sats1.kod +
uttryck3.kod +
instruktion("goto " + före_testet) +
instruktion(efter_loopen + ":");
}
För att skapa kod för en stackmaskin:
sats -> for ( uttryck1 ; uttryck2 ; uttryck3 ) sats1
{
string före_testet = new_label();
string efter_loopen = new_label();
sats.kod =
uttryck1.kod +
instruktion("label" + före_testet) +
uttryck2.kod +
instruktion("jumpfalse " + efter_loopen) +
sats1.kod +
uttryck3.kod +
instruktion("jump " + före_testet) +
instruktion("label" + efter_loopen);
}
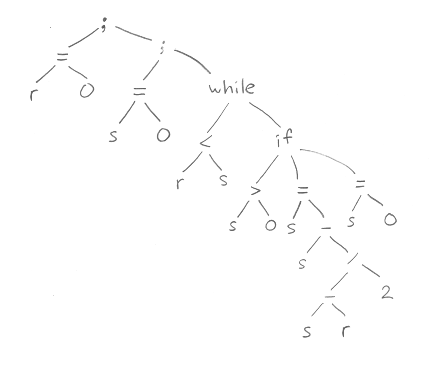
b) postfixkod för en stackmaskin
lvalue r
push 0
=
lvalue s
push 100
=
label 1:
rvalue r
rvalue s
<
gofalse 2
rvalue s
push 0
>
gofalse 3;
lvalue s
rvalue s
rvalue s
rvalue r
-
push 2
/
-
=
goto 4
label 3:
lvalue s
push 0
=
label 4:
goto 1
label 2:
c) treadresskod
r = 0;
s = 100;
label 1:
if (r >= s) goto 2;
if (s <= 0) goto 3;
temp1 = s - r;
temp2 = temp1 / 2;
temp3 = s - temp2;
s = temp3;
goto 4;
label 3:
s = 0;
label 4:
goto 1;
label 2:
Ett basic block är en följd av kod (typiskt treadressinstruktioner) som alltid utförs i en följd, dvs det finns inga hopp in i blocket (annat än till dess första instruktion), och blocket innehåller inga hoppinstruktioner (annat än eventuellt den sista instruktionen).
b) (4p)
Flera olika typer av optimeringar kan göras på koden inuti ett enskilt basic block. Här är några:
Rättningskommentar: Två exempel, bra beskrivna med kod, räcker för full poäng.
| -> |
|
| -> |
|
| -> |
|
| -> |
|
| -> |
|
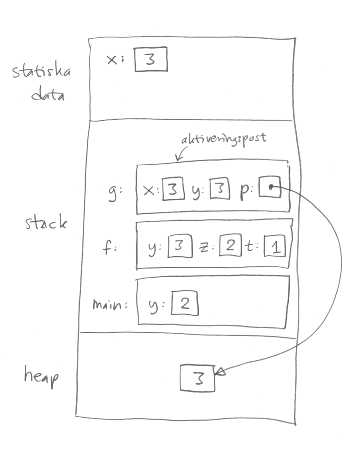
Den globala variabeln x finns, och finns på samma plats, under hela programkörningen, så den placeras i den del av minnet där statiska data lagras. Statiska data betyder inte att de inte ändras, utan att deras placering och storlek inte ändras.
I aktiveringsposten för en funktion, till exempel f,
lagras funktionens lokala variabler (för funktionen f är det variabeln t),
och dess parametrar (y o
Med malloc reserverar man minne på heapen,
som sedan måste avallokeras antingen manuellt (med free)
eller med hjälp av en skräpsamlare.
I verkligheten kan det också finnas temporära variabler i funktionerna,
och en del variabler kan ligga i processorregister i stället för i primärminnet.
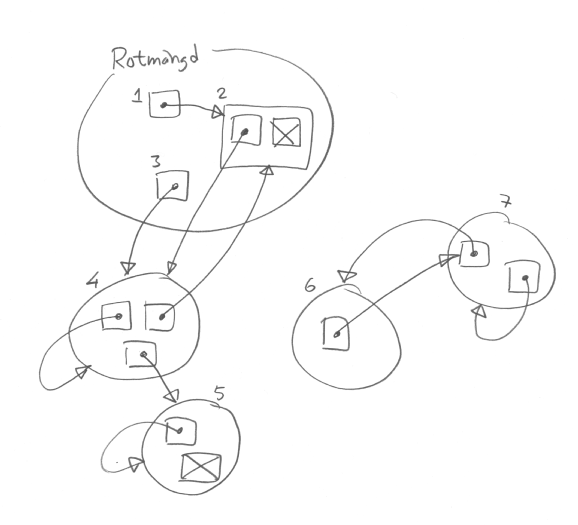
Här har vi några minnesobjekt.
Objekt 1-3 finns i rotmängden och ska inte tas bort,
för vi antar att de är direkt nåbara från programmet,
till exempel
genom att vara globala variabler eller lokala variabler i funktioner.
Med terminologin från uppgit 8 utgörs rotmängden av stacken och statiska data.
Objekt 4-7 ska skräpsamlas,
och tas bort om de inte går att nå via pekare från rotmängden.
Med terminologin från uppgit 8 finns dessa på heapen.
Objekt 4 och 5 går att nå, så de kanske kommer att användas igen,
men objekt 6 och 7 vet vi att de aldrig mer kommer att användas (eftersom de alltså inte går att komma åt).
Därför ska objekt 6 och 7 tas bort.
För mark and sweep krävs det att varje objekt har en flagga som markerar om det är använt eller inte.
Skräpsamlaren körs lite då och då.
Vi börjar med att gå igenom alla objekten i hela minnet, och sätta flaggan till falsk.
(Det krävs alltså att det finns ett sätt för skräpsamlaren att nå alla objekt i minnet,
även om det vanliga programmet inte kan det.)
Sen kommer markeringsfasen. Vi går igenom alla objekten i rotmängden.
(Det krävs alltså att det finns ett sätt för skräpsamlaren att systematiskt gå igenom objekten i rotmängden.)
För varje objekt vi besöker sätter vi flaggan till sann (vilket alltså betyder att objektet används),
och följer sen alla pekare från det objektet, och besöker de objekt som pekarna pekar på.
(När vi kommer till ett objekt som har flaggan satt, vet vi att det redan är besökt,
och låter därför bli att göra något mer med det.)
Genom att på detta sätt rekursivt besöka objekt,
kommer vi att besöka alla objekt som går att nå från rotmängden.
Sen kommer sopfasen.
Vi går igenom alla objekten i hela minnet, och för varje objekt undersöker vi flaggan.
Är flaggan satt så besöktes objektet i markeringsfasen, och är alltså nåbart, och ska vara kvar.
Är flaggan inte satt så besöktes objektet inte i markeringsfasen, och vi vet då att det inte är nåbart,
så det ska rensas bort, och dess minne kan återanvändas.
Fördelar jämfört med referensräkning:
Uppgift 9: Run-time-omgivningar (5 p)
Nackdelar (med dem enkla, grundläggande mark-and-sweep-algoritmen) jämfört med referensräkning:
Thomas Padron-McCarthy
(Thomas.Padron-McCarthy@tech.oru.se)
3 november 2006