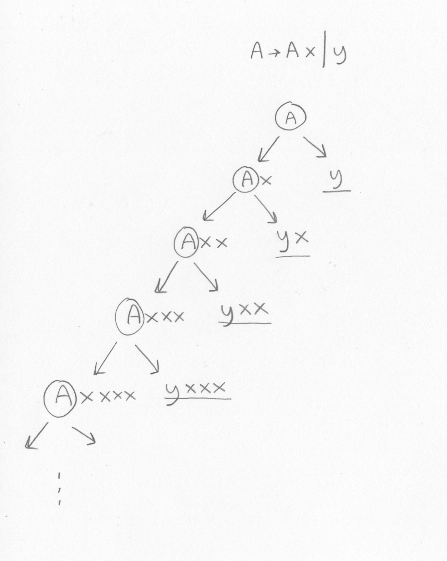
This paper is about how you sometimes have to re-write a grammar in order to write a parser.
Before reading this section, you should already be able to answer these questions:
The steps in summary:
expression -> expression + term | term term -> id | numThe grammar is left-recursive. It contains this left-recursive production:
If we write a predictive recursive-descent parser based on the grammar, it will contain a procedure called expression, which begins as follows:expression -> expression + term
void expression() {
if (lookahead == num or lookahead == id) {
expression(); match('+'); term();
}
else
...
What happens?
Assume the following source program:
This source program will scan the scanner to the following token sequence:2 + 2 + 2;
When we begin to parse the source program, the first num is the current token, or lookahead token.num + num + num ;
When entering the function expression it turns out that lookahead is equal to num. Thus, we enter the first branch of the if statement, and we call the function expression.
When entering the function expression it turns out that lookahead is equal to num. Thus, we enter the first branch of the if statement, and we call the function expression.
When entering the function expression it turns out that lookahead is equal to num. Thus, we enter the first branch of the if statement, and we call the function expression.
...
Because no tokens are consumed, the parser will be stuck on the first num. No tokens are consumed, and therefore the program is stuck in an endless recursion.
Other types of parsers, such as those created by the Yacc tool, can handle left-recursive productions, but a recursive-descent parser of the type we see here can't. So you have to write about the grammar.
A left-recursive production can easily be rewritten as a couple of other rules that are not left-recursive. Suppose the grammar looks like this:
A is a non-terminal, but x and y can stand for arbitrary constructions, with multiple terminals and non-terminals.A -> A x | y
The rule is replaced by the following two rules, which describe the same language but are not left recursioned:
A -> y R R -> x R | empty
Example: This left-recursive grammar,
can be rewritten to this, which is not left recursion recursive:expression -> expression + term | term
In this example, A , x , y and R corresponded to:expression -> term rest rest -> + term rest | empty
What language does this grammar describe? Or, put differently, what programs can you generate from it?A -> A x | y
We assume that A is the start symbol. We can generate all allowed programs by repeatedly expanding the non-terminals. There will be a tree that looks like this (but note that this is not a parse tree or a syntax tree, but it is a tree that shows what the grammar allows):
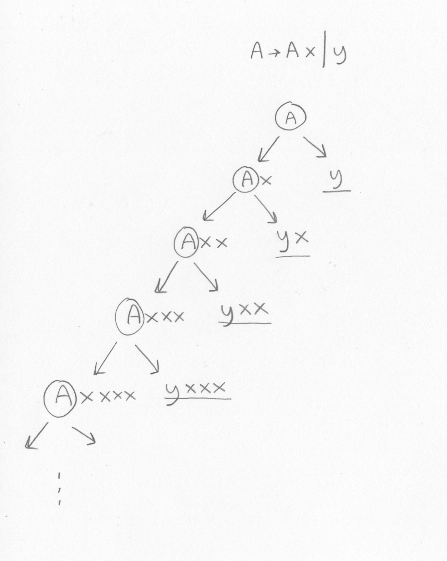
The underlined expressions can not be expanded. We see a pattern: What this grammar describes are programs consisting of a y followed by zero, one or more x .
In the previous section we said that we could write the left recursion grammar to the following grammar, which describes the same language but is not left-recursive:
If all is correct then it should also describe programs consisting of a y followed by zero, one or more x:A -> y R R -> x R | empty
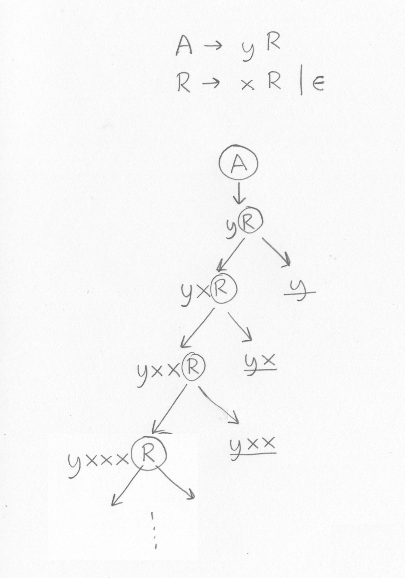
For example, the following source programs should be allowed: 2, 2+3, 2-3, 2-3+4+5-6
ASU-86 Figure 2.13 / 2.19 shows the translation scheme (ie a grammar of semantic inputs) based on:
expression -> expression + term { print('+') }
expression -> expression - term { print('-') }
expression -> term
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
(Remember that a rule like
term
->
term
+
term
gives an ambiguous grammar, so we transformed the grammar. We have also
seen how to handle operator associativity and operator priority.)
Now we re-write the grammar to eliminate the left recursion.
Important: You should handle the semantic
actions as part of the grammar, as you re-write it according to the
above technique for eliminating left recursion!
Otherwise, the prints will end up in the wrong place.
The result will look like this:
expression -> term rest
rest -> + term { print('+') } rest
rest -> - term { print('-') } rest
rest -> empty
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
The two rules for addition and subtraction were both left recursive, and have therefore been transformed.
In the case of the rule for addition,
A,
x,
y
and
R
corresponded to:
void term () {
if (isdigit(lookahead)) {
putchar(lookahead);
match(lookahead);
}
else
error();
}
void rest() {
if (lookahead == '+') {
match('+'); term(); putchar('+'); rest();
}
else if (lookahead == '-') {
match('-'); term(); putchar('-'); rest();
}
else
;
}
void expression() {
term(); rest();
}
The full source code:
2.5
Suppose, for example, that a captain can call four different commands to her soldiers: "halt", "forward march", "fire" and "fire cease". It can be described with the following grammar:
(Note that in reality, in English, the command to cease fire is cease fire, not fire cease, but this example is adapted from Swedish, where the words are in the other order!)command -> halt command -> forward march command -> fire command -> fire cease
If you are a soldier and hear the captain shout forward, you know that the command that the captain is calling will be forward march.
But if you hear the captain calling a command that starts with fire, you can't yet know if the command is fire or fire cease. You have to wait until you hear the next word.A soldier might be able to solve it by waiting for a while to see what the captain says after fire. A recursive-descent parser is in a worse situation because it has a procedure for each non-terminal, and in that procedure, the parser selects which production that the non-terminal is to be expanded using, by executing the branch in an if-statement that corresponds to that production. What code should it run if it doesn't know which one is the right one?
If you find an identifier, such as a, in the source program, at a point where a statement is to be used, then you do not know if that is the beginning of an assignment or of an expression.statement -> assignment | expression assignment -> id = uttryck <-- Always starts with id expression -> term more-terms <-- Can start with id ...
| Found in the source program | Followed by | That means "a" is the beginning of ... |
|---|---|---|
| a |
= 5 ...
+ 5 ... |
An assignment
An expression |
This case can be handled with two-token lookahead, ie not only looking at the current token but also the next, instead of the one-token lookahead.
But that solution does not always work. For example, if we have a little more advanced grammar, similar to the language C, which allows assignments such as a[7] = 8 and a[i + 2] = 8, it two-token lookahead does not help:
| Found in the source program | Followed by | That means "a" is the beginning of ... |
|---|---|---|
| a[3+4+z] |
= 5 ...
+ 5 ... |
An assignment
An expression |
So we may need any number of tokens lookahead.
What you do instead is to try one of the rules, and if it turns out that
that rule could not be used then you go back ("backtrack") and try
instead with the other.
That is difficult to do with a C program, but it is possible.
But it's worse than that. It is not enough to remember a single choice, which you may have to go back to and change, but there may be several choices after each other before we know if the first choice was right or wrong.
For example, in a real C program, we can write an assignment such as a[b[3] = 9] = 8 assignments, which means that we first put the value 9 in position 3 in the array b, and then we take the value of the assignment expression, which is 9 (if b is an integer array) and uses it as index in array a, ie we place value 8 in position 9 in the array a.
| Found in the source program | Followed by | That means "a" is the beginning of ... |
|---|---|---|
| a[b[5+6] |
= 5 ...
+ 5 ... |
An assignment
An expression |
So we get a tree of choices, and we have to keep track of how far back in the tree we are going to go back.
Other types of parsers, such as those created by the Yacc tool, can handle a grammar that contains FIRST() conflicts, but a recursive-descent parser of the type we see here can't. So you have to re-write the grammar.
An example of FIRST() conflict is this grammar, which describes an if statement with an optional else branch:
statement -> if ( expression ) statement
| if ( expression ) statement else statement
Do you remember the trick to remove left recursion? A similar method, left factorization, can be used to remove a FIRST() conflict. You can re-write the grammar as follows:
Here's how to do left-factorization. Re-write these two (yes, two) productions:statement -> if ( expression ) statement optional-else-branch optional-else branch -> else statement | empty
to these three (yes, three) productions:A -> xy | xz
Before you can write a predictive recursive-descent parser, you should rewrite its grammar so that it:A -> x R R -> y | z
But for simple grammar, like a calculator or a search field on a webpage, you sometimes need to write the parser yourself, by hand. It may be difficult to plug in Yacc in an ASP page or Perl script.
Look at the following example, where search phrases, with keywords, or, and, and parentheses, has to be translated into SQL queries to be run against a database with which words are contained in which documents.
| Search phrase | SQL query |
|---|---|
| cinema |
select d.Nr
from Document d, Occurs o, Word w where d.Nr = o.Document and o.Word = w.Number and w.Text = 'cinema' |
| cinema Örebro |
select Document.Nr
from Document d, Occurs o1, Occurs o2, Word w1, Word w2 where (d.Nr = o1.Document and o1.Word = w1.Number and w1.Text = 'cinema') and (d.Nr = o2.Document and o2.Word = w2.Number and w2.Text = 'Örebro') |
| (cinema or museum) and Örebro |
select Document.Nr
from Document d, Occurs o1, Occurs o2, Occurs o3, Word w1, Word w2, Word w3 where ((d.Nr = o1.Document and o1.Word = w1.Number and w1.Text = 'cinema') or (d.Nr = o2.Document and o2.Word = w2.Number and w2.Text = 'Örebro')) and (d.Nr = o3.Document and o3.Word = w3.Number and w3.Text = 'Örebro') |