Kompilatorer och interpretatorer: Tentamen 2017-01-04

Örebro universitet
Institutionen för naturvetenskap och teknik
Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se)

Tentamen i

Kompilatorer och interpretatorer

för Dataingenjörsprogrammet m fl

onsdag 4 januari 2017

Gäller som tentamen för:
DT3030 Datateknik C, Kompilatorer och interpretatorer, provkod 0100

Hjälpmedel:	Inga hjälpmedel.
Poängkrav:	Maximal poäng är 40. För godkänt betyg krävs totalt minst 23 poäng, varav minst 8 poäng på uppgift 1.
Resultat:	Meddelas på kursens hemsida eller via e-post senast torsdag 26 januari 2017.
Återlämning av tentor:	Elektroniskt via Studentforum.
Examinator och jourhavande:	Thomas Padron-McCarthy, telefon 070 - 73 47 013.

Skriv tydligt och klart. Lösningar som inte går att läsa kan naturligtvis inte ge några poäng. Oklara och tvetydiga formuleringar kommer att misstolkas.
Skriv den personliga tentamenskoden på varje inlämnat blad. Skriv inte namn eller personnummer på bladen.
Skriv bara på en sida av papperet. Använd inte röd skrift.
Antaganden utöver de som står i uppgifterna måste anges.
Skriv gärna förklaringar om hur du tänkt. Även ett svar som är fel kan ge poäng, om det finns med en förklaring som visar att huvudtankarna var rätt.

LYCKA TILL!

Formelsamling

1. Eliminering av vänsterrekursion

En vänsterrekursiv grammatik kan skrivas om så att den inte är vänsterrekursiv. Antag att en regel (eller, korrektare uttryckt, två produktioner), i grammatiken ser ut så här:

A -> A x | y

A är en icke-terminal, men x och y står för godtyckliga konstruktioner som består av terminaler och icke-terminaler.

Regeln ersätts av följande två regler (eller, korrektare uttryckt, tre produktioner), som beskriver samma språk men som inte är vänsterrekursiva:

A -> y R
R -> x R | empty

2. Vänsterfaktorisering

Antag att grammatiken innehåller denna regel (två produktioner):

A -> x y | x z

A är en icke-terminal, men x, y och z står för godtyckliga konstruktioner som består av terminaler och icke-terminaler.

Skriv om till dessa tre produktioner:

A -> x R
R -> y | z

Uppgift 1 (10 p)

En kompilators arbete brukar delas in i ett antal faser. Ange vilka det är, och förklara kort vad varje fas gör. Vad är in- och utdata från respektive fas?

Uppgift 2 (5 p)

Antag att minnet innehåller dessa sexton dataobjekt. Pilarna är pekare, och kryss betyder NULL-pekare. De inringade objekten, nummer 1-6, utgör rotmängden.

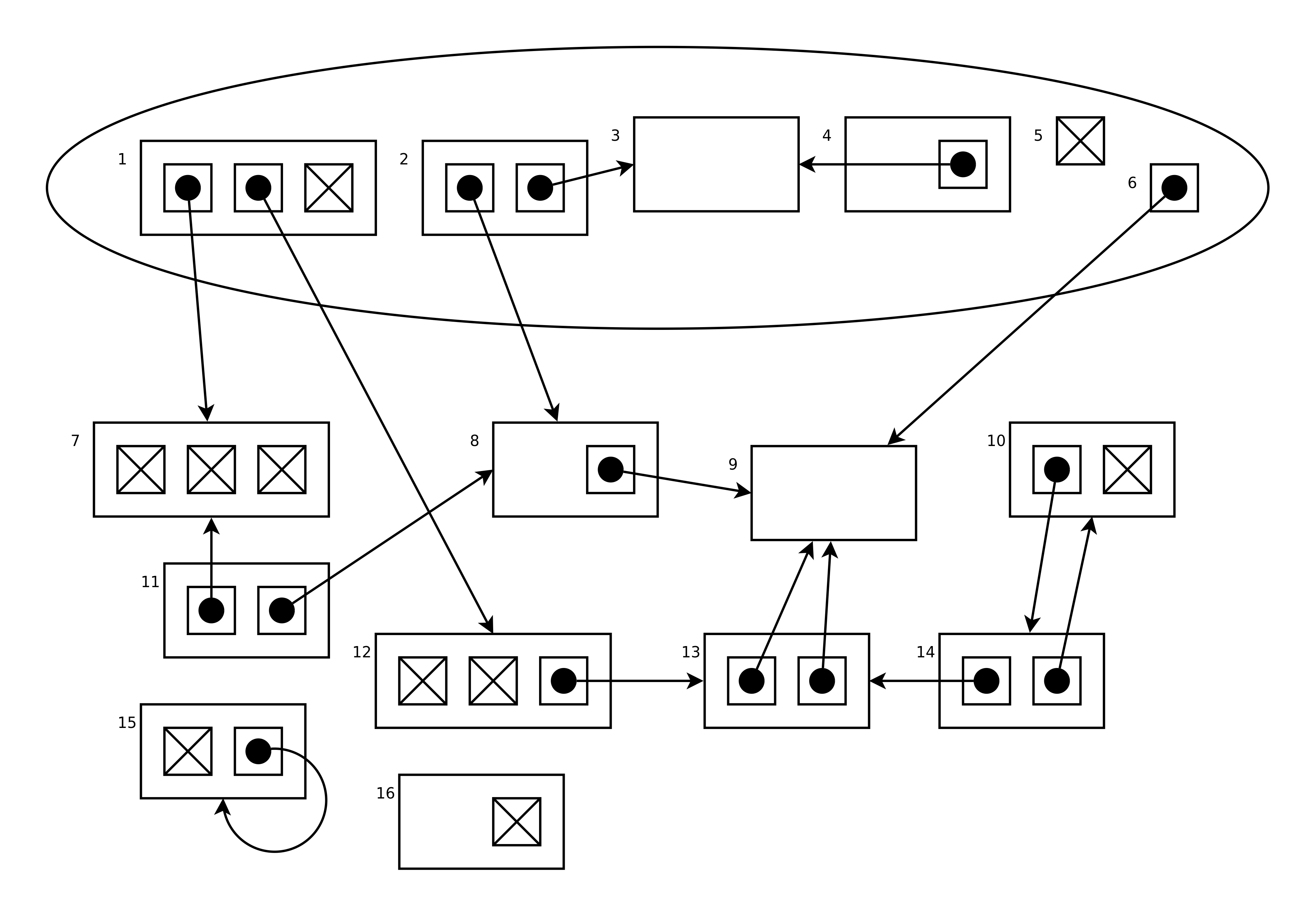
Några dataobjekt

a) Vi använder skräpsamlingsmetoden "mark and sweep". Vilka av objekten kommer att markeras i markeringsfasen?

b) Vilka objekt kommer att städas bort i sopfasen?

c) Vilka objekt kommer att finnas kvar efter sopfasen?

d) Antag att vi i stället använder referensräkning. Är det några av objekten som skulle städats bort i sopfasen i delfråga b ovan, som inte kommer att kunna städas bort med referensräkning? Vilka?

Uppgift 3 (3 p)

Det här är ett programavsnitt i ett C-liknande språk:

    b = a * 2 + a * 3 * 4;
    c = a * 2;
    a = d;
    e = a * 2;
    
    while (a * 2 < f * 4) {
        e = a * 2;
        f = f + 1;
    }

Översätt ovanstående programavsnitt till en av följande två typer av mellankod.

a) ett syntaxträd, även kallat abstrakt syntaxträd (genom att rita upp trädet!)

b) postfixkod för en stackmaskin

Observera: Det finns två deluppgifter i uppgiften ovan. Välj ut och besvara (högst) en av dessa. (Skulle du svara på båda, räknas den med högst poäng bort.)

Uppgift 4 (6 p)

a) Översätt programavsnittet från uppgiften ovan till treadresskod, och rita upp den i form av en flödesgraf.

b) Visa vilka optimeringar en maskinoberoende optimerare kommer att göra på treadresskoden. Visa både hur optimeringen går till och slutresultatet.

Scenario till de övriga uppgifterna

Satslogik är, som Wikipedia skriver, ett formellt logiskt system med väldefinierad syntax, avsett att symboliskt hantera språkliga satser, vilka uttrycker påståenden. Vi vill bygga ett system för att hantera satslogik, och det första steget är att skriva programkod som kan läsa formler.

En formel i satslogiken är uppbyggd av satser och så kallade konnektiv (som också skulle kunna kallas operatorer). En sats anges med en ensam bokstav, till exempel p och q. Det finns fem konnektiv, nämligen:

negation, som anges med tecknet ¬
konjunktion, som anges med tecknet ∧
disjunktion, som anges med tecknet ∨
implikation, som anges med tecknet →
ekvivalens, som anges med tecknet ↔

Negation verkar på en enda delformel och sätts före den, som i ¬ p, medan de övriga binder samman två delformler, som i p ∧ q.

Det finns ingen allmänt accepterad prioritetsordning mellan konnektiven, så för att undvika tvetydigheter ska vi gruppera konnektiven med parenteser.

Några exempel på giltiga formler:

p
p ∧ q
¬(p ∧ q)
(¬p) ∧ q
(p ∧ q) ∨ r
p ∧ (q ∨ r)
(p ∧ (q ∨ r))
(p ∧ (¬ q)) → r
p ↔ (¬ p)

Några exempel på formler som inte är giltiga:

p ∧ q ∨ r
¬p ∧ q

Uppgift 5 (2 p)

Ange vilka terminaler, dvs typer av tokens, som behövs för att man ska kunna skriva en grammatik för formler i satslogiken.

Uppgift 6 (4 p)

Skriv en grammatik för formler i satslogiken. Startsymbolen ska vara formel, som representerar en formel enligt scenariot ovan.

Uppgift 7 (3 p)

Ett parse-träd (ibland kallat "konkret syntaxträd") innehåller noder för alla icke-terminaler. Rita upp parse-trädet för den här formeln, enligt din grammatik i uppgiften ovan:

(p ∧ (¬ q)) → r

Uppgift 8 (7 p)

Skriv en prediktiv recursive-descent-parser för formler i satslogiken, i ett språk som åtminstone liknar C, C++, C# eller Java. Du behöver inte skriva exakt korrekt programkod, men det ska framgå vilka procedurer som finns, hur de anropar varandra, och vilka jämförelser med tokentyper som görs. Du kan anta att det finns en funktion som heter scan, som returnerar typen på nästa token, och en funktion som heter error, som man kan anropa när något gått fel och som skriver ut ett felmeddelande och avslutar programmet.