Observera att detta är förslag på lösningar. Det kan finnas andra lösningar som också är korrekta, och det kan hända att en del av lösningarna är mer omfattande än vad som krävs för full poäng på uppgiften.
Expression -> TermEller, mer kompakt skrivet:
Expression -> Expression union Term
Expression -> Expression minus Term
Term -> Faktor
Term -> Term intersection Faktor
Faktor -> Set
Faktor -> left_parenthesis Expression right_parenthesis
Set -> Literal
Set -> Variable
Literal -> left_bracket Elements right_bracket
Literal -> left_bracket right_bracket
Elements -> Elements comma integer
Elements -> integer
Variable -> identifier
Expression -> Term | Expression union Term | Expression minus Term
Term -> Faktor | Term intersection Faktor
Faktor -> Set | left_parenthesis Expression right_parenthesis
Set -> Literal | Variable
Literal -> left_bracket Elements right_bracket | left_bracket right_bracket
Elements -> Elements comma integer | integer
Variable -> identifier

b)
(Man kan systematiskt gå igenom alla strängar som går att härleda genom att börja med S och sen tillämpa reglerna i grammatiken.)
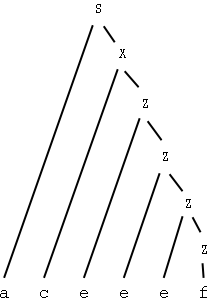
Förutom aa och ad matchas (om jag räknat rätt) samma strängar som matchas av det reguljära uttrycket ace*fb*.
Några strängar: aa, ad, acf, acef, aceef, aceeef, aceeeef, aceeeeef, aceeeeeef, aceeeeeeef, aceeeeeeeef, acfb, acefb, aceefb, aceeefb, aceeeefb, aceeeeefb, aceeeeeefb, aceeeeeeefb
c)
Grammatiken innehåller två produktioner för S:
där FIRST(a X) och FIRST(a Y) båda är lika med { a }. Därför kan en prediktiv parser inte välja vilken regel som ska användas, i alla fall inte med en enda tokens lookahead.S -> a X S -> a Y
Produktionen
innehåller vänsterrekursion. En recursive-descent-parser som parsar en sträng, och ska matcha icke-terminalen X, anropar proceduren X. I den proceduren avgörs att källsträngen matchar högerledet X b. Därefter ska det högerledet matchas, och vi börjar med att matcha X genom att anropa proceduren X. Och nu är vi alltså tillbaka i samma procedur, utan att ha "förbrukat" några tokens i inmatningen, och så håller det på i en oändlig rekursion.X -> X b
d)
Den generella transformationen vänsterfaktorisering:
A -> x y | x z
blir
A -> x R
och
R -> y | z
I vårt fall:
S -> a X | a Y
blir
S -> a R1
och
R1 -> X | Y
Den generella transformationen eliminering av vänsterrekursion:
A -> A x | y
blir
A -> y R
och
R -> x R | empty
I vårt fall:
X -> X b | c Z
blir
X -> c Z R2
och
R2 -> b R2 | empty
Den transformerade grammatiken:
empty ska egentligen vara symbolen för en tom sträng, men den är svår att skriva i HTML så det blir rätt i alla webbläsare.S -> a R1 R1 -> X | Y X -> c Z R2 R2 -> b R2 | empty Y -> a | d Z -> e Z | f
e)
void error() {
printf("Ledsen error.\n");
exit(EXIT_FAILURE);
}
void match(int expected) {
if (lookahead != expected)
error();
else
lookahead = scan();
}
extern void S(), R1(), X(), R2(), Y(), Z();
void S() {
printf("S\n");
match('a');
R1();
}
void R1() {
printf("R1\n");
if (lookahead == 'c')
X();
else if (lookahead == 'a' || lookahead == 'd')
Y();
else
error();
}
void X() {
printf("X\n");
match('c');
Z();
R2();
}
void R2() {
printf("R2\n");
if (lookahead == 'b') {
match('b');
R2();
}
else {
/* Match empty */
}
}
void Y() {
printf("Y\n");
if (lookahead == 'a') {
match('a');
}
else if (lookahead == 'd')
match('d');
else
error();
}
void Z() {
printf("Z\n");
if (lookahead == 'e') {
match('e');
Z();
}
else if (lookahead == 'f')
match('f');
else
error();
}
void parse() {
printf("parse\n");
lookahead = scan();
S();
}