Observera att detta är förslag på lösningar. Det kan finnas andra lösningar som också är korrekta, och det kan hända att en del av lösningarna är mer omfattande än vad som krävs för full poäng på uppgiften.
Årtal: 1[0-9][0-9][0-9]
Klädstorlekar: XS|S|M|L|XL
Eller M|X*(S|L), så matchar man även t ex XXXXXXL
Däremot är X?[SML] fel, eftersom det matchar XM
b) (2p)
[0-9][0-9][0-1][0-9][0-3][0-9]-[0-9][0-9][0-9][0-9]
Kontrollerar inte att månaden är högst 12, utan månaden kan vara upp till 19. Kontrollerar inte att dagen är högst 31, utan dagen kan vara upp till 39. Kontrollerar inte att kontrollsiffran stämmer med formeln.
c) (1p)
En token är den abstrakta entitet som består av en tokentyp, exempelvis heltal, och ett lexikaliskt värde, exempelvis att det är heltalet 64. Ett lexem är den teckensekvens i källprogrammet som scannern tolkade som en token. I det här fallet kan det ha varit teckensekvensen 64, men också till exempel 0100, som i C tolkas som ett oktalt tal eftersom den börjar med 0.
a) vänsterrekursion
Grammatik:
tilltal -> dumheter mamma
dumheter -> empty
dumheter -> dumheter dumma
Anta att en prediktiv recursive-descent-parser ska parsa tokensekvensen dumma dumma mamma som ett tilltal. Först anropas proceduren tilltal, och den i sin tur anropar proceduren dumheter, med den första dumma som lookahead-token.
void dumheter() {
if (lookahead == dumma) {
dumheter(); match(dumma);
}
else {
/* Matchar tomma strängen - vi gör inget */
}
}
Eftersom lookahead är dumma går vi (helt korrekt) in i den första grenen i if-satsen, och den börjar (helt korrekt) med ett anrop till proceduren dumheter. Så vi anropar proceduren dumheter, fortfarande med den första dumma som lookahead-token.
Eftersom lookahead är dumma går vi (helt korrekt) in i den första grenen i if-satsen, och den börjar (helt korrekt) med ett anrop till proceduren dumheter. Så vi anropar proceduren dumheter, fortfarande med den första dumma som lookahead-token.
Och så har vi fastnat i en oändlig rekursion, eftersom vi inte förbrukar några tokens med match.
En lösning på problemet är att använda en annan typ av parser, som inte har problem med vänsterrekursion. En annan lösning är att skriva om grammatiken för att eliminera vänsterrekursionen. Det finns en enkel kokboksregel för detta. Den nya grammatiken beskriver samma språk, men är inte längre vänsterrekursiv. Den ursprungliga grammatiken skrivs om från:
Den nya, efter eliminering av vänsterrekursionen:A -> A x | y
A -> y R R -> x R | empty
I vårt fall:
tilltal -> dumheter mamma
dumheter -> R
R -> dumma R
R -> empty
Eller om man förenklar lite:
tilltal -> dumheter mamma
dumheter -> dumma dumheter
dumheter -> empty
b) FIRST()-konflikter
Grammatik:
kommando -> halt
kommando -> eld
kommando -> eld upphör
En prediktiv recursive-descent-parser utan backtracking och med bara en tokens lookahead kan, när den ser en token eld, inte veta om det är början på kommandot eld eller på kommandot eld upphör. Eftersom parsern har en if-sats (eller motsvarande) med olika grenar för eld och eld upphör, vet den inte vilken av grenarna den ska gå in i:
void kommando() {
if (lookahead == halt) {
match(halt);
}
else if (lookahead == eld) {
match(eld);
}
else if (lookahead == eld) {
match(eld);
match(upphör);
}
}
En lösning på problemet är att använda en annan typ av parser, som inte har problem med FIRST()-konflikter. En annan lösning är att skriva om grammatiken för att eliminera FIRST()-konflikten. Det finns en enkel kokboksregel, vänsterfaktorisering. Den nya grammatiken beskriver samma språk, men har inte längre FIRST()-konflikten. Den ursprungliga grammatiken skrivs om från:
Den nya:A -> x y | x z
A -> x R R -> y | z
I vårt fall kan det bli så här:
kommando -> halt
kommando -> eld eld-fortsättning
eld-fortsättning -> empty | upphör
c) tvetydighet
Grammatik:
uttryck -> tal
uttryck -> uttryck - uttryck
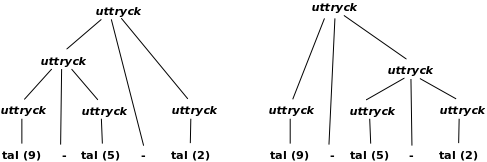
Anta att vi ska parsa källprogrammet 9-5-2, som motsvarar tokensekvensen tal - tal - tal Det spelar ingen roll vilken typ av parser vi använder.
9-5-2 kan nu ge upphov till två olika parse-träd, som båda stämmer med grammatiken:

Det första trädet motsvarar (9-5)-2, som blir 2 och som överensstämmer med de vanliga räknereglerna. Det andra trädet motsvarar 9-(5-2), som blir 6.
Här finns (förstås!) ingen enkel kokboksregel, utan vi måste välja vilket parse-träd som är det som vi vill ha, och sen skriva om grammatiken så den bara tillåter det trädet. Med vårt exempel kan det bli så här, om vi vill att de vanliga aritmetikreglerna ska gälla:
uttryck -> uttryck - tal
uttryck -> tal
x = 1;
y = 2;
z = 3;
while (y == 2) {
if (z > 4) {
y = y - 1 - 1;
}
else {
z = z + y * z + z;
t = t + 2;
}
}
Översätt ovanstående programavsnitt till
två av följande tre typer av mellankod.
a) ett abstrakt syntaxträd (genom att rita upp trädet!)
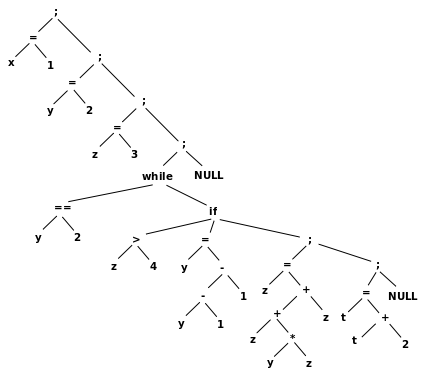
b) postfixkod för en stackmaskin
lvalue x
push 1
=
lvalue y
push 2
=
lvalue z
push 3
=
label 1:
rvalue y
push 2
==
gofalse 2
rvalue z
push 4
>
gofalse 3
lvalue y
rvalue y
push 1
-
push 1
-
=
goto 4
label 3:
lvalue z
rvalue z
rvalue y
rvalue z
*
+
rvalue z
+
=
lvalue t
rvalue t
push 2
+
=
label 4:
goto 1
label 2:
c) treadresskod
x = 1;
y = 2;
z = 3;
label 1:
if (y ≠ 2) goto 2;
if (z ≤ 4) goto 3;
temp1 = y - 1;
temp2 = temp1 - 1;
y = temp2; // Eller direkt, utan tempvariabeln
goto 4;
label 3:
temp3 = y * z;
temp4 = z + temp3;
temp5 = temp4 + z;
z = temp5; // Eller direkt, utan tempvariabeln
temp6 = t + 2;
t = temp6; // Eller direkt, utan tempvariabeln
label 4:
goto 1
label 2:
| Observera: Det finns tre deluppgifter i uppgiften ovan. Välj ut och besvara (högst) två av dessa. (Skulle du svara på alla tre, räknas den med högst poäng bort.) |
a) målspråk
Det språk som målprogrammet, dvs det program som kompilatorn genererar som sina utdata, ska vara skrivet i. Ofta assemblerkod eller maskinkod för en fysisk eller virtuell maskin. C förekommer också som målspråk.
b) målprogram
Det program som kompilatorn genererar som sina utdata.
c) front end
Den "halva" av kompilatorn som arbetar med källprogrammet, till skillnad från en back end, som genererar målprogrammet. De faser som ingår kan vara scanner, parser, semantisk analysator, mellankodsgenerator och maskinoberoende optimering.
d) Yacc
Ett välkänt verktyg (från 1970-talet) som översätter en grammatik för ett språk till en parser för det språket. Nästan helt kompatibel med GNU Bison, som är ett nyare verktyg.
e) symboltabell
En datastruktur där kompilatorn lagrar namnen på variabler, procedurer, datatyper med mera, tillsammans med information om dessa. Första gången kompilatorn ser ett namn i källprogrammet, som antal_smurfer, läggs det in i symboltabellen. Nästa gång kompilatorn ser antal_smurfer, kan det slå upp det namnet i symboltabellen. Även reserverade ord (se nedan) kan finnas i symboltabellen.
f) shift-reduce-konflikt
En bottom-up-parser arbetar med en stack. På den stacken kan den "skifta" in tokens från det parsade källprogrammet. Om det överst på stacken finns en eller flera tokens och icke-terminaler som enligt en produktion i grammatiken kan reduceras till en icke-terminal, kan parsern också reducera dessa tokens och icke-terminaler till den icke-terminalen. Ibland kan båda dessa operationer (skifta och reducera) vara giltiga enligt grammatiken, och då har man en shift-reduce-konflikt. En shift/reduce-konflikt beror ofta på att grammatiken är tvetydig, men den kan också bero på att den parsern bara har en enda tokens lookahead när den bestämmer hur den ska tolka indata. En del grammatiker kräver mer lookahead, och ger därför shift/reduce-konflikter trots att de inte är tvetydiga.
g) deterministisk ändlig tillståndsmaskin
Tillståndsmaskiner (kallas även "automater") är ett sätt att beskriva beteenden. Tillståndsmaskinen befinner sig i ett av flera olika tillstånd, och varje gång den får indata av något slag byter den till ett annat (eller samma) tillstånd. En ändlig (kallas även "finit") tillståndsmaskin har ett ändligt antal tillstånd. I en deterministisk tillståndsmaskin byter man alltid till ett visst tillstånd från ett visst tillstånd vid ett visst indata, till skillnad från en icke-deterministisk tillståndsmaskin där det kan finnas flera olika övergångar för ett givet tillstånd och ett givet indata.
Varje reguljärt uttryck kan beskrivas som en deterministisk ändlig tillståndsmaskin.
h) reserverat ord
En identifierare som har en viss, fix betydelse i grammatiken och inte kan användas som namn på variabler och annat. Vanliga exempel är if och while.
i) anropskonventioner (på engelska: call sequence)
Den sekvens av operationer (maskinkodsinstruktioner) som ett program utför vid anrop av en procedur, och var den koden ska läggas (vid anropsstället eller i den anropade proceduren). Varje processorarkitektur, eller ibland varje operativsystem, eller ibland varje kompilator, har en konvention för hur detta ska göras. Bland det som ska göras är att spara undan processorns register och tillstånd i minne på stacken, och att överföra argument och returvärden.