Grammatiktransformationer

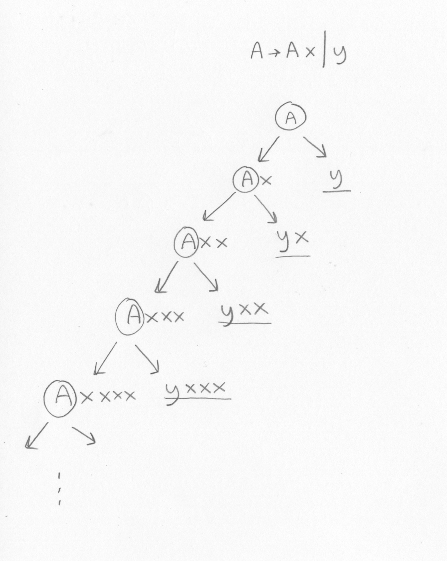
Det här avsnittet handlar om hur man ibland måste skriva om sin grammatik för att kunna skriva en parser.

Innan du läser det här avsnittet bör du kunna följande:

• Vad är en grammatik, och hur fungerar den?
• Vad betyder orden terminal, icke-terminal och produktion?
• Vad innebär parsning? Vad menas med källprogram, källspråk och parse-träd?
• Vad är en parser?
• Vad är menas med aktuell token (på engelska: current token eller lookahead token)?
• Vad är en recursive-descent-parser? Hur fungerar den?
• Vad är en prediktiv recursive-descent-parser? Hur fungerar den?
• Hur skriver man en prediktiv recursive-descent-parser, utgående från en grammatik?
• Vad innebär det att en grammatik är tvetydig?
• Vad är ett syntax-styrt översättningsschema (på engelska: syntax-directed translation scheme)?

Att skriva en prediktiv recursive-descent-parser

Stegen i sammanfattning:

1. Skriv en grammatik som beskriver det källspråk du vill parsa.
2. Är grammatiken tvetydig? I så fall måste du först bestämma vilken av betydelserna som är den rätta, och sen skriva om grammatiken så att den bara tillåter den betydelsen. (Exempel: Ska 3-4-5 tolkas som (3-4)-5, som blir -6, eller som 3-(4-5), som blir 4?)
3. Om parsern ska göra något mer än bara kontrollera att källprogrammet följer grammatiken, måste du stoppa in semantiska aktioner som gör det du vill göra. Det kan vara att beräkna värdet av uttryck, att generera kod, eller något annat.
4. Innehåller grammatiken FIRST()-konflikter? I så fall måste du skriva om grammatiken, så att FIRST()-konflikterna försvinner.
5. Innehåller grammatiken vänsterrekursion (vilket kommer att förklaras strax vad det är)? I så fall måste du skriva om grammatiken, så att vänsterrekursionen försvinner?
6. Konstruera en prediktiv recursive-descent-parser utifrån grammatiken.

Vad är vänsterrekursion, och varför är det dåligt?

uttryck -> uttryck + term | term
term -> id | num

uttryck -> uttryck + term

void uttryck() {
  if (lookahead == num or lookahead == id) {
    uttryck(); match('+'); term();
  }
  else
...  

Antag följande källprogram:

2+2+2;

num + num + num ;

När funktionen uttryck anropas, visar det sig att lookahead är lika med num. Alltså går vi in i den första grenen i if-satsen, och vi anropar funktionen uttryck.

När funktionen uttryck anropas, visar det sig att lookahead är lika med num. Alltså går vi in i den första grenen i if-satsen, och vi anropar funktionen uttryck.

När funktionen uttryck anropas, visar det sig att lookahead är lika med num. Alltså går vi in i den första grenen i if-satsen, och vi anropar funktionen uttryck.

...

Eftersom inga tokens förbrukas, "står parsern och stampar" på det första num. Inga tokens förbrukas, och därför fastnar programmet i en oändlig rekursion.

Andra typer av parsers, till exempel en sådan som skapas av verktyget Yacc, klarar av vänsterrekursiva regler, men en recursive-descent-parser av den typ vi sett här klarar det inte. Alltså måste man skriva om grammatiken.

Eliminering av vänster-rekursion

En vänsterrekursiv regel kan enkelt skrivas om till ett par andra regler, som inte är vänsterrekursiva. Antag att grammatiken ser ut så här:

A -> A x | y

Regeln ersätts av följande två regler, som beskriver samma språk men som inte är vänsterrekursiva:

A -> y R
R -> x R | empty

Exempel: Den här vänsterrekursiva grammatiken,

uttryck -> uttryck + term | term

uttryck -> term rest
rest -> + term rest | empty

• A = uttryck
• x = + term
• y = term
• R = rest

Expansion av icke-terminaler med hjälp av grammatikens produktioner

A -> A x | y

Vi antar att det är A som är startsymbol. Vi kan generera alla tillåtna program genom att gång på gång expandera icke-terminalerna. Det blir ett träd som ser ut så här (men notera att detta inte är ett parse-träd eller ett syntaxträd, utan det är ett träd som visar vad grammatiken tillåter):

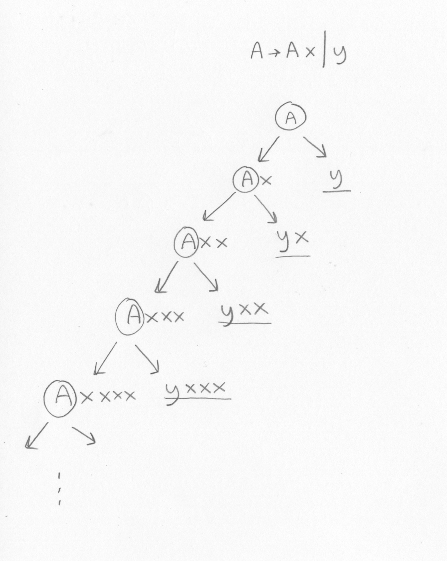
De understrukna uttrycken kan inte expanderas vidare. Vi ser ett mönster: Det som den här grammatiken beskriver är program som består av ett y följt av noll, ett eller flera x.

I förra avsnittet sa vi att vi kunde skriva om den vänsterrekursiva grammatiken till följande grammatik, som beskriver samma språk men som inte är vänsterrekursiv:

A -> y R
R -> x R | empty

Ett exempel på eliminering av vänster-rekursion

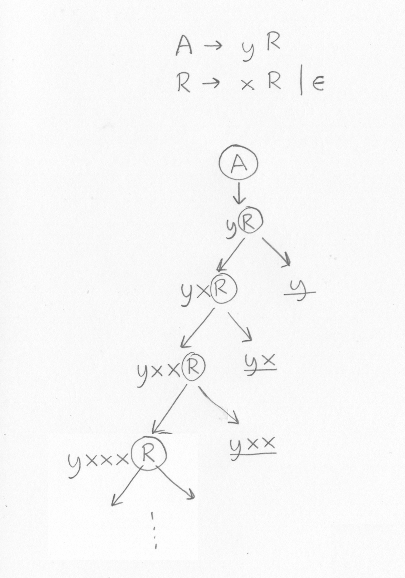
Exempelvis ska följande källprogram kunna parsas: 2, 2+3, 2-3, 2-3+4+5-6

ASU-86 figur 2.13/2.19 visar det översättningsschema (dvs en grammatik med inlagda semantiska aktioner) som man utgår från:

uttryck -> uttryck + term { print('+') }
uttryck -> uttryck - term { print('-') }
uttryck -> term
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }

Nu skriver vi om grammatiken för att eliminera vänsterrekursionen.
Viktigt: Man ska hantera de semantiska aktionerna som en del av grammatiken, när man skriver om den enligt tekniken ovan för eliminering av vänsterrekursion! Annars kommer utskrifterna att hamna på fel plats.

Så här blir resultatet:

uttryck -> term rest
rest -> + term { print('+') } rest
rest -> - term { print('-') } rest
rest -> empty
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }

• A = uttryck
• x = + term { print('+') }
• y = term
• R = rest

• A = uttryck
• x = - term { print('-') }
• y = term
• R = rest

void term () {
  if (isdigit(lookahead)) {
    putchar(lookahead);
    match(lookahead);
  }
  else
    error();
}

void rest() {
  if (lookahead == '+') {
    match('+'); term(); putchar('+'); rest();
  }
  else if (lookahead == '-') {
    match('-'); term(); putchar('-'); rest();
  }
  else
  ;
}

void uttryck() {
  term(); rest();
}

Vad är en FIRST()-konflikt, och varför är det dåligt?

Antag som exempel att en kapten kan ropa fyra olika kommandon till sina soldater: "halt", "framåt marsch", "eld" och "eld upphör". Det kan beskrivas med följande grammatik:

kommando -> halt
kommando -> framåt marsch
kommando -> eld
kommando -> eld upphör

En soldat kan kanske lösa det där genom att vänta en stund och se vad kaptenen ropar efter att ha ropat eld. En recursive-descent-parser har det värre, för den har ju en procedur för varje icke-terminal, och i procedureren väljer parsern vilken produktion som icke-terminalen ska expanderas med genom att köra den gren i en if-sats som motsvarar den produktionen. Vad ska den köra för kod om den inte vet vilken som är rätt?

Svårigheter att hantera FIRST()-konflikter

sats -> tilldelning | uttryck
tilldelning -> id = uttryck       <-- Börjar alltid med id
uttryck -> term fler-termer        <-- Kan bärja med id
...

Just det här fallet kan hanteras med två-tokens-lookahead, dvs att man tittar inte bara på aktuell token utan även på nästa, i stället för en-tokens-lookahead.

Men den lösningen fungerar inte alltid. Om vi till exempel har en lite mer avancerad grammatik, som påminner mer om språket C, och som tillåter tilldelningar av typen a[7] = 8 eller a[i+2] = 8, så hjälper det inte med två-tokens-lookahead:

Vi kan alltså behöva hur många tokens lookahead som helst.
Det man gör i stället är att pröva med en av reglerna, och om det (till sist) visar sig att den regeln inte gick att använda, så går man tillbaka ("backtrackar") och försöker i stället med den andra. Det är krångligt att göra med ett C-program, men det går.

Men det är värre än så. Det räcker inte alltid med att komma ihåg ett enda val, som man kanske måste gå tillbaka till och ändra, utan det kan komma flera val efter varandra, innan vi vet om det första valet var rätt eller fel.

Exempelvis kan vi i ett riktigt C-program kan vi skriva tilldelningar av typen a[b[3] = 9] = 8, som betyder att först placerar vi värdet 9 i position 3 i arrayen b, och sen tar vi värdet av det tilldelningsuttrycket, som är 9 (om b är en heltalsarray) och använder som index i arrayen a, dvs vi placerar värdet 8 i position 9 i arrayen a.

Vi får alltså ett träd av valmöjligheter, och vi måste hålla reda på hur långt tillbaka i det trädet vi ska gå tillbaka.

Andra typer av parsers, till exempel en sådan som skapas av verktyget Yacc, klarar av grammatiker som innehåller FIRST()-konflikter, men en recursive-descent-parser av den typ vi sett här klarar det inte. Alltså måste man skriva om grammatiken.

Vänsterfaktorisering