A computer language is a language that is designed with the intension that it should be read and understood by computers. It may be a programming language like C ++, Java or Visual Basic, but it can also be a much easier language, such as describes what to write in a configuration file, or what can be entered in an entry box.
A grammar for a language describes the language, and describes how to put together sentences and other constructions in that language.
There are also natural languages like Swedish and English. The natural languages tend to be much more free than the computer language, so that you for example can change the word order. The boundary between right and wrong is more fluid in natural languages.
Because computers are much stupider than people, one must be much more careful when writing something that a computer should read and understand. A person can often understand an opinion even though there is a comma in the wrong place. But if you type a comma in the wrong place in a program, then your computer will mostly do either nothing at all, or something completely different from what you thought.
The grammar for the language English says, for example, that one can make a sentence for example by first writing a noun and then a verb, and finish with a period. That rule could be written as follows:
sentence -> noun verb .
You can thus take any noun, followed by a any verb, and a period, and this forms a sentence.
Because natural languages like English are quite free, it is difficult or impossible to write a complete and correct grammar that really does describe everything you can say in English.
It is much easier to write a grammar for a computer language. Computer languages are much simpler than natural languages, and moreover, they are much more precisely specified. There are no (well, almost none) doubtful cases, but if you write something in a computer language like Java, it's either right or wrong. Not as in English, where you can talk quite a long time about whether an expression is right or wrong, and in the end it may prove to be a matter of taste.
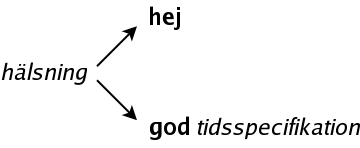
greeting -> hi | good morning | good afternoon | good evening
A greeting can be either
hello,
good morning,
good afternoon or
good evening.
The symbol "|"
means "or".
The symbol "->" can be read as "can be replaced with" or "can be expanded to".
Here is another grammar that describes the exact same language:
greeting -> hi | good time_specification
time_specification -> morning | afternoon | evening
A greeting is either
hello or the word
good, followed by a time_specification, and the time_specification can be either
morning,
afternoon or
evening.
Instead of using the "or" sign "|" to show that a time_specification can be one of several different things, you can write several different rules:
greeting -> Hi
greeting -> good time_specification
time_specification -> morning
time_specification -> afternoon
time_specification -> evening
In grammar, we also use the names greetings and time_specification. They do not appear in the greeting language, but only in the grammar. They are called non-terminals, and we write them in italics.
A "terminal" is something that is at the end of something. At the end of a bus line there is a bus terminal. There the bus stops, and the passengers leave. If we have a non-terminal, such as greeting, we can continue and replace it, according to the rules of grammar, but when we arrive at a terminal, such as tomorrow, we can not replace it with anything else, and we have to stop there.
A production is a rule in the grammar, which states that a certain non-terminal can be replaced with something else. For example, this is a production that says that non-terminal greetings can be replaced by the terminal good followed by the non-terminal time_specification:
greeting -> good time_specification
Also note that this is not
one production, but
three:
The "or" sign "|" is just a shorter way to write several different productions. Instead of the above, you can print the three productions like this:tidsspecifikation -> morgon | afternoon | evening
time_specification -> morning time_specification -> afternoon time_specification -> evening
When writing a grammar, it is not enough to specify which terminals, non-terminals and productions there are, but you must also indicate what kind of things you want to say in the language, for example, if you are saying complete greetings or just time specifications. To do this, we specify a start symbol.
For our greeting language, it is greeting that is the start symbol, not time_specification.
When we talk about a language we mean the set of all allowed sequences of terminals. This simple language contains four such sequences, but a language like C ++ contains of course many more - maybe even infinitely many.
The figures have noot been translated yet, and still use the Swedish terminals and non-terminals!
There are two ways to expand it:
hello can not be expanded, so we will not go on, but the non-terminal time_specification can be expanded in three different ways:
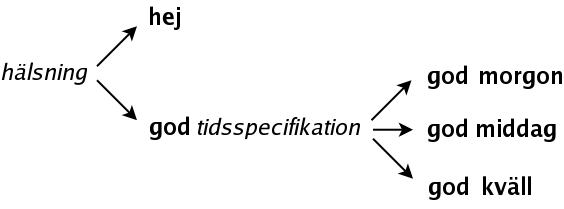
Now we can go no further.
We have formed a tree, and the language, ie, which sequences of terminals are allowed, we find by looking at the leaves in the tree.
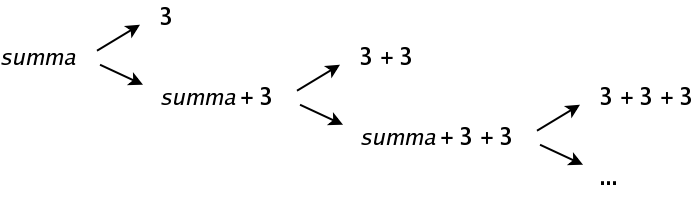
Although the grammar of this language contains only two terminals, one non-terminal and two productions, the language contains infinitely many allowed sequences:
There are several ways to write such a grammar, but we choose to think like this: A sum is either a lone number, or you have a sum (which may be a lone number) where you add a new number at the end, so that there will be a new sum.
A first try:
Then the grammar becomes even shorter:
Now it may be a bit clearer how we thought: A sum is either a lone number, or you have a sum (which may be a lone number), attaching a plus sign and a new number at the end, making it a new sum.
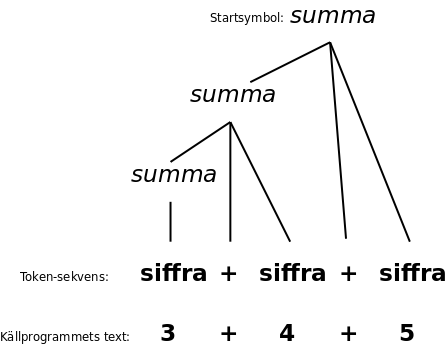
The source program to be compiled usually consists of text, ie a sequence of characters:
x = lower_coordinate + 14;The scanner reads the source program text, and instead creates a sequence of terminals, or "tokens", which are passed on to the parser:
identifier, equals sign, identifier, plus sign, integer, semicolonNote that the spaces disappeared because they have no meaning, they are just used to separate the terminals, and also note several characters (such as 1 and 4 ) can form a single terminal.
Normally, the scanner also sends information about which identifiers and integers it found, like this:
identifier (x), equals sign, identifier (lower_coordinate), plus sign, integer (14), semicolonThe parser reads this sequence of tokens, compares it to the grammar, and determines if there is an allowed sequence of tokens according to the grammar, and which of the productions in grammar are needed to generate this sequence.
When designing a compiler, one can sometimes choose whether to place a certain amount of work in the scanner or in the parser. For example, we saw above that you could have the parser rule a rule that says a "number" is 0 to 9, or you could let the scanner recognize that 0 to 9 are numbers.
(A parenthesis: It's not really true that the parser necessarily builds a parse tree. Sometimes it doesn't build a tree, at least not as a data structure in memory. Instead, the parser goes through the productions in grammar in an order so that it could build a parse tree.)
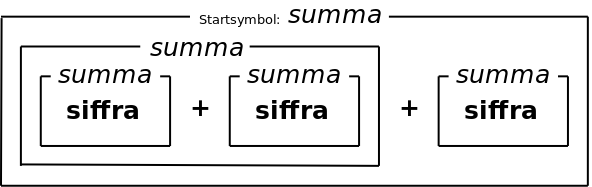
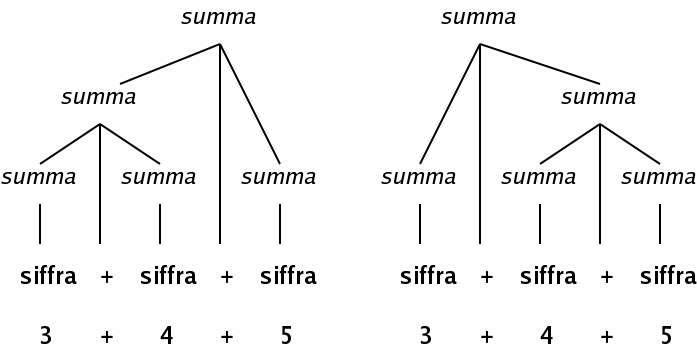
The parse tree shows what the things (such as sums) consist of. For example, a sum can consist of two other sums. Therefore, instead of a tree you can draw it as boxes, with boxes inside boxes:
One can simplify the parse tree by (1) removing the internal nodes that only have a single sub-node, and (2) moving operators to the node above where they replace the non-terminal:
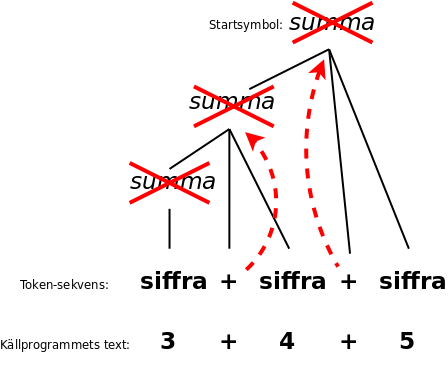
Then a so-called syntax tree is formed, sometimes called an abstract syntax tree:
The simpler syntax contains all the information needed to calculate the expression (or run the program), but does not contain the information about the grammar structure found in the parse tree.
Another way of thinking is this: A sum is either a lone number, or two sums that you add:
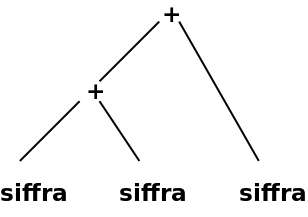
That a grammar is ambiguous means that the same sequence of tokens can be described by (at least) two different parse trees, according to the grammar. Note how 3 + 4 + 5 can be described in two ways:
If you group the additions with parentheses, this corresponds to the two expressions (3+4)+5 and 3+(4+5) respectively.
For addition the result will be the same. Both sums yield the result 12, as an addition always gives the same result regardless of the order in which the terms are added. But if we had subtraction instead of addition, then the two expressions would have been (3-4)-5 and 3-(4-5). They give completely different results.
The opposite of ambiguous grammar is a unique grammar. A grammar for a computer language should be unambiguous, because an ambiguous grammar makes it possible for a source program to be interpreted in different ways, and it is difficult for the computer to know, with some sort of "common sense", which of the different interpretations was intended by the programmer.
An initial attempt to write the grammar:
The same grammar can also be written as follows, if you want to write it more compactly:
That's an ambiguous grammar (try it yourself!). Next attempt:
It's better, but it only fits expressions on the form numbers * numbers + numbers * numbers.
We want to multiply arbitrarily many numbers into one term, and add many terms to an expression arbitrarily. Then both the term rule and the expression rule must handle it. We use what we learned earlier about how to combine sums by constantly adding + numbers to a sum.
%token number
%start expression
%%
factor : number ;
term : factor | term '*' factor ;
expression : term | expression '+' term ;
%%
|
You can also type the parser by hand, using maybe fifty lines of program code in a language like C or Java. (If you know how to do it. If you don't know how to do it, you might need a thousand lines, resulting in a program that only almost works.)