Observera att detta är förslag på lösningar. Det kan finnas andra lösningar som också är korrekta, och det kan hända att en del av lösningarna är mer omfattande än vad som krävs för full poäng på uppgiften.
De vanligaste typerna av fel:
Expr -> Term | Expr '+' Term | Expr '-' Term
Term -> Faktor | Term '*' Faktor | Term '/' Faktor
Faktor -> number | '(' Expr ')' | sin '(' Expr ')' | cos '(' Expr ')'

b) 2p
c) 2p
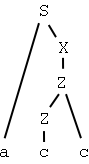
Produktionen
innehåller vänsterrekursion. En recursive-descent-parser som parsar en sträng, och ska matcha icke-terminalen Z, anropar proceduren Z. I den proceduren avgörs om källsträngen matchar högerledet Z b. Det sker genom att de olika delarna av högerledet matchas, och vi börjar med att matcha Z genom att anropa proceduren Z. Och nu är vi alltså tillbaka i samma procedur, utan att ha "förbrukat" några tokens i inmatningen, och så håller det på i en oändlig rekursion.Z -> Z c
d) 4p
Eliminering av vänsterrekursion:
A -> A x | y
blir
A -> y R
och
R -> x R | empty
(Fel svar:
A -> A x | x
blir
A -> x R
och
R -> x R | empty.
Det är bara i just den här grammatiken som det råkar vara så att x = y.)
I vår grammatik kommer regeln
Z -> Z c | catt omvandlas till de två reglerna
Z -> c R
R -> c R | empty
e) 7p
En del av felkontrollerna i nedanstående program är redundanta. Kontrollen av att det inmatade uttrycket är slut behöver inte vara med. Spårutskrifterna, som skriver ut namnen på icke-terminaler, behöver inte heller vara med.
int lookahead;
void error() {
printf("Ledsen error.\n");
exit(EXIT_FAILURE);
}
void match(int expected) {
if (lookahead != expected)
error();
else
lookahead = scan();
}
extern void S(), X(), Y(), Z(), R();
void S() {
printf("S\n");
match('a');
X();
}
void X() {
printf("X\n");
if (lookahead == 'a' || lookahead == 'b')
Y();
else if (lookahead == 'c')
Z();
else
error();
}
void Y() {
printf("Y\n");
if (lookahead == 'b') {
match('b');
Y();
match('b');
}
else if (lookahead == 'a')
match('a');
else
error();
}
void Z() {
printf("Z\n");
match('c');
R();
}
void R() {
printf("R\n");
if (lookahead == 'c') {
match('c');
R();
}
else {
/* Match empty */
}
}
void parse() {
printf("parse\n");
lookahead = scan();
S();
match('$'); /* End of expression */
printf("Ok.\n");
}
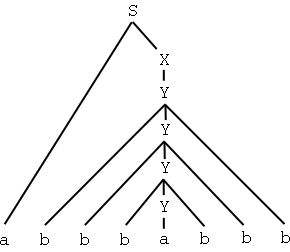
Grammatiken innehåller regeln
Y -> b Y b | aDen motsvaras av alla strängar som består av ett a omgivet av lika många b på varje sida. Eftersom reguljära uttryck inte tillåter rekursion, och inte har någon annan mekanism för att "komma ihåg" saker från en del av ett uttryck till ett annat, går det inte att skriva ett reguljärt uttryck för det.
(En kommentar: Det spelar ingen roll om man använder den givna grammtiken, eller den som man själv modifierat. Förutsatt att man har gjort rätt beskriver de ju samma språk.)
Här är ett härledningsträd för vilka strängar som kan härledas ur startsymbolen S:
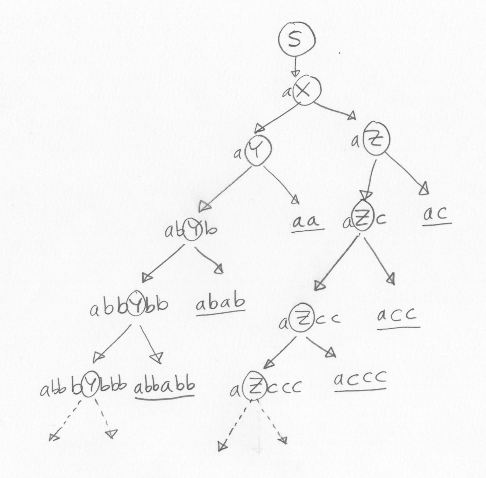
Det reguljära uttrycket (ab*ab*)|(acc*) (eller motsvarande) är fel svar på uppgiften, eftersom det alltså måste vara lika många b på varje sida om a, och det kan man inte ange med ett reguljärt uttryck, men det svaret ger ändå två poäng.
Att bara svara nej på frågan och hänvisa till att grammatiken är rekursiv räcker inte. Exempelvis kan den rekursiva grammatiken S -> S a | b skrivas som det reguljära uttrycket ba*.
Att man kan bilda två eller flera olika parse-träd för samma token-sekvens.
b) 2p
Denna grammatik matchar bland annat strängen 3 + 3 + 3.Uttryck -> Uttryck + Uttryck | 3
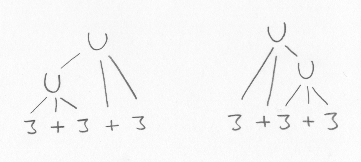
c) 2p
Tvetydigheten är ett problem om de olika parse-träden betyder olika saker. Om de inte betyder olika saker, är tvetydigheten förmodligen inte ett problem.
Exempel:
Här kan strängen 3 - 3 - 3 tolkas antingen som uttrycket (3 - 3) - 3, vilket beräknas till -3, eller som 3 - (3 - 3), vilket blir 3. Här är det alltså viktigt att grammatiken är entydig, och att parsern alltid tolkar uttrycket på samma (korrekta) sätt, för annars kan ju resultatet bli fel.Uttryck -> Uttryck - Uttryck | 3
Ett annat exempel är en grammatik som beskriver sekvenser av en eller flera stjärnor (till exempel för recensioner av biofilmer):
Grammatiken är tvetydig, men här spelar det inte så stor roll om *** tolkas som två stjärnor följt av en stjärna, eller en stjärna följt av två stjärnor.Stjärnor -> Stjärnor Stjärnor | *
(Ett annat och helt rimligt svar på uppgift c är att tvetydighet alltid är ett problem, eftersom det skapar svårigheter när vi ska skriva parsern.)
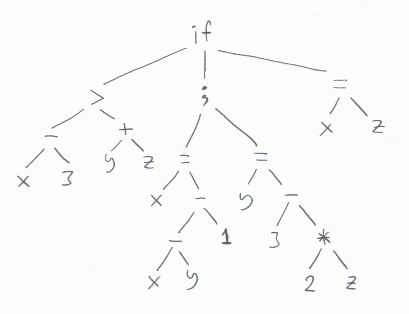
Andra lösningar är möjliga för att representera blocket med de två satserna.
b) 3.5p
rvalue x
push 3
minus
rvalue y
rvalue z
plus
greaterthan
jumpfalse ELSE
lvalue x
rvalue x
rvalue y
minus
push 1
minus
assign
lvalue y
push 3
push 2
rvalue z
multiply
minus
assign
goto AFTER_ELSE
ELSE: lvalue x
rvalue z
assign
AFTER_ELSE:
c) 3.5p
t1 = x - 3
t2 = y + z
if (t1 ≤ t2) goto ELSE
t3 = x - y
t4 = t3 - 1
x = t4
t5 = 2 * z
t6 = 3 - t5
y = t6
goto AFTER_ELSE;
ELSE: x = z;
AFTER_ELSE:
Egentligen ska varje inre nod i ett uttryck bli en temporärvariabel,
men man kan också göra vissa optimeringar direkt i genereringen av mellankod:
t1 = x - 3
t2 = y + z
if (t1 ≤ t2) goto ELSE
t3 = x - y
x = t3 - 1
t4 = 2 * z
y = 3 - t4
goto AFTER_ELSE;
ELSE: x = z;
AFTER_ELSE:
Statement -> for identifier = Expression1 to Expression2 do Statement1
{
string limit = new_temporary_variable();
string before = new_label();
string after = new_label();
Statement.code =
Expression1.code +
instruction(identifier.place + " = " + Expression1.place) +
Expression2.code +
instruction(limit.place + " = " + Expression2.place) +
instruction(before + ":") +
instruction("if " + identifier.place + " > " + limit.place +
" goto " + after) +
Statement1.code +
instruction(identifier.place + " = " +
identifier.place + "+" + "1") +
instruction("goto " + before) +
instruction(after + ":");
}
Vi antar att funktionerna new_label och new_temporary_variable
genererar ett nytt, unikt namn på en label respektive på en variabel.
Som exempel skulle satsen
kunna generera (den o-optimerade) kodenfor i = 2 to 5 do Writeln(i)
t1 = 2
i = t1
t2 = 5
t3 = t2
label1: if i > t3 goto label2
param i
call Writeln, 1
i = i + 1
goto label1
label2:
a) 3p
Varje objekt som ska kunna skräpsamlas innehåller en referensräknare, som helt enkelt är en (liten) variabel som anger hur många pekare det finns till objektet. Varje gång man ändrar innehållet i en pekarvariabel i programmet, måste man justera dessa referensräknare. Referensräknaren i det objekt som pekaren pekar på efter ändringen ska ökas med ett, och referensräknaren i det objekt som pekaren pekade på före ändringen ska minskas med ett. Om referensräknaren i ett objekt stegas ner till noll, vet man att det objektet inte längre har några pekare till sig. Det kan därför aldrig mer nås, utan är skräp och kan avallokeras eller återanvändas.
Det är fel svar att skriva att räknandet av referenser sker "när skräpsamlaren körs". Referensräknaren uppdateras direkt i samband med att en pekare ändras. Periodiskt återkommande skräpsamlingar är en egenhet hos mark-and-sweep, inte hos normal referensräkning.
Det är också fel svar att skriva att objekten tas bort "nästa gång skräpsamlaren körs". Normalt tas ett objekt bort direkt när dess referensräknare gått ner till noll, omedelbart efter att en pekare ändrades.
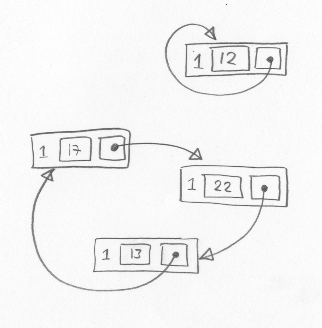
b) 2p
Cirkulära datastrukturer. Följande fyra poster, som är tänkta som element i en länkad lista, har inga pekare till sig och kan därför aldrig mer nås av programmet, men var och en av posterna har fortfarande en referens till sig, och kan därför inte återanvändas om man använder vanlig referensräkning.