Kursen Kompilatorer och interpretatorer | Föreläsningar: 1 2 3 4 5 6 7 8 9 10 11 12
Det här är ungefär vad jag tänker säga på föreläsningen. Använd det för förberedelser, repetition och ledning. Det är inte en definition av kursinnehållet, och det ersätter inte kursboken.
Idag: Att skriva en parser för hand
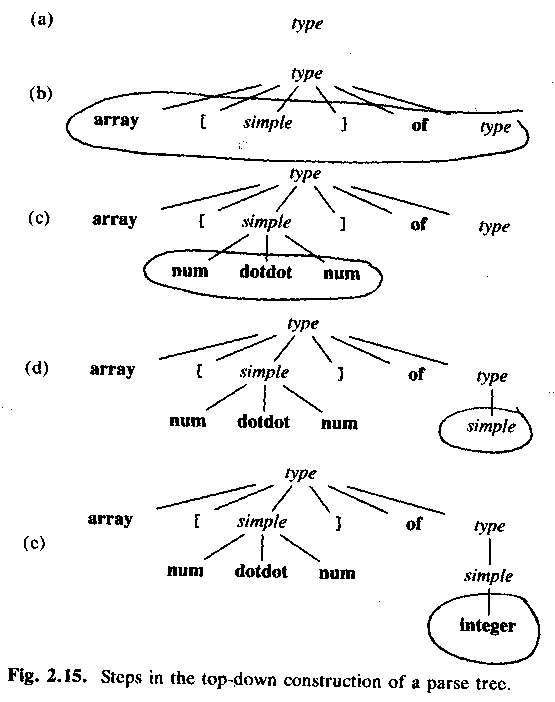
Ex: Types in Pascal.
Examples:simple -> integer simple -> char simple -> num dotdot num type -> simple type -> ^ id type -> array [ simple ] of type
Example source program:integer 1..100 ^kundpost array [ integer ] of char array [ 20..40 ] of 0..3 array [ 1..5 ] of array [ 1..3 ] of 2..5
Tokens:
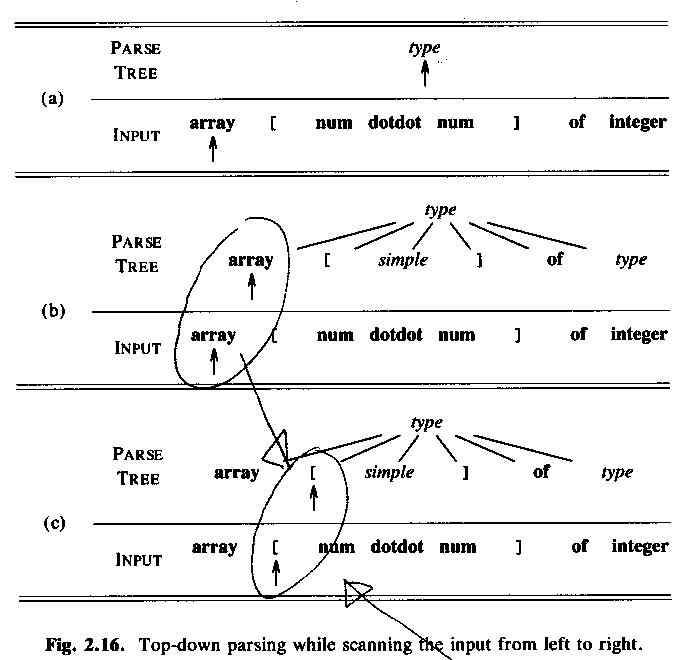
array [ num dotdot num ] of integer
Top-down parsing, starting with a node for the non-terminal type.
Which of the productions (=rules) should we use? (Answer: type -> array ....)
Why? (Answer: The only production that starts with array.)
"Lookahead symbol" = "current token" = Sw: "aktuell token"
ASU-86 fig 2.15:

ASU-86 fig 2.16:
If always just one production possible to chose: predictive parsing, no backtracking
Recursive-descent parsing = the parser is a program with a procedure (in C: "function") for each non-terminal.
void simple() {
if (lookahead == integer)
match(integer);
else if (lookahead == char)
match(char);
else if (lookahead == num) {
match(num); match(dotdot); match(num);
}
else
error();
}
match() checks that the lookahead symbol (=current token) is the expected one,
and gets the next token (by calling the lexical analyzer).
When we write the function type(), it is not enough to see which tokens occur as the first token in the productions for type (^ and array). Since simple can occur as the first thing in a type, we must also see which tokens occur as the first token in productions for simple.
void type() {
if (lookahead == integer or lookahead == char or lookahead == num)
simple();
else if (lookahead == ^) {
match(^); match(id);
}
else if (lookahead == array) {
match(array); match([); simple(); match(]); match(of); type();
}
else
error();
}
FIRST(x) = all possible first tokens in strings that match x.
FIRST(simple) = the set { integer, id, char }
FIRST(^ id) = the set { ^ }
FIRST(array [ simple ] of type) = the set { array }
FIRST(type)
= the set { ^, array } + the set FIRST(simple)
= the set { ^, array, integer, id, char }
Recursive-descent without backtracking: if the grammar contains two rules...
...then FIRST(something) and FIRST(somethingelse) must be disjoint (=no common elements).NT -> something NT -> somethingelse
Use opt_stmts -> empty if nothing else matches opt_stmts, which will be when lookahead is end.stmt -> begin opt_stmts end opt_stmts -> stmt_list | empty
Implementation of a predictive, recursive-descent parser:expr -> expr + term
void expr() {
if (lookahead == num or lookahead == id)
expr();
else
...
Eliminate left recursion!
Rewrite this left-recursive production:
(A, x och y är bara platshållare. A står för en icke-terminal, medan x och y står för sekvenser av både terminaler och icke-terminaler. I boken används grekiska bokstäver: A -> A α | β)A -> A x | y
into these, which are not left-recursive:
(Vi kan visa att båda dessa grammatiker beskriver samma språk, nämligen ett y följt av noll, ett eller flera x, genom att Systematiskt expandera startsymbolen A i båda grammatikerna.)A -> y R R -> x R | empty
Example: rewrite this left-recursive production:
into these, which are not left-recursive:expr -> expr + term | term
A = exprexpr -> term rest rest -> + term rest | empty
Första versionen: Ett uttryck är antingen en term, eller så har man redan ett uttryck (som kan innehålla en eller flera termer) och gör ett nytt uttryck genom att lägga till ett plustecken och en term.
Andra versionen: Ett uttryck består av en term, följt av en rest. Denna rest kan antingen vara tom (så att uttrycket bara bestod av den där enda termen), eller så består den av ett plustecken och en term, följt av ytterligare en rest (som kan vara tom eller innehålla en eller flera termer).
|
Men, varning!
Den nya, omskriva grammatiken innehåller ju andra produktioner än originalet. Därför blir det förstås ett annat parse-träd som skapas för ett visst uttryck! Bland annat har +-operatorn nu blivit högerassociativ i stället för vänsterassociativ! (Rita upp de två olika parse-träden för term + term + term, om vi låtsas att term är en terminal.) Men, som vi ska se i nästa avsnitt: Om man har en grammatik med inbäddade semantiska aktionerna (dvs ett så kallad syntax-styrt översättningsschema), så kan man också flytta runt de semantiska aktionerna i transformationen, och då kommer de att göras i rätt ordning.) |
Ex: 2, 2+3, 2-3, 2-3+4+5-6
ASU-86 Fig 2.13/2.19 translation scheme for the program in 2.5:
expr -> expr + term { print('+') }
expr -> expr - term { print('-') }
expr -> term
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
Remember that term -> term + term was ambiguous
(Sw: tvetydig), so we transformed the grammar.
Rewrite the grammar to eliminate left recursion.
Important: Handle the semantic actions as part of the grammar,
when you rewrite it using the left-recursion elimination technique from above,
to get the prints done at the right places!
expr -> term rest
rest -> + term { print('+') } rest
rest -> - term { print('-') } rest
rest -> empty
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
The interesting parts of the program:
void term () {
if (isdigit(lookahead)) {
putchar(lookahead);
match(lookahead);
}
else
error();
}
void rest() {
if (lookahead == '+') {
match('+'); term(); putchar('+'); rest();
}
else if (lookahead == '-') {
match('-'); term(); putchar('-'); rest();
}
else
;
}
void expr() {
term(); rest();
}
Full source code: 2.5
| Resten handlar om Program 2.9. |
For example, when the source being read contains fnord, a call to lexan() will return 259 (which is the value ID, meaning that we have found an identifier), and put (for example) 16 in the variable tokenval, meaning that the identifier that was found is identifier number 16 in the symbol table.
Source code: lexer.c
Source code: symbol.c
Remember how stack macines work:
Kursen Kompilatorer och interpretatorer | Föreläsningar: 1 2 3 4 5 6 7 8 9 10 11 12