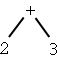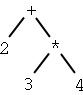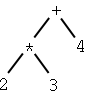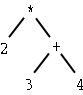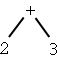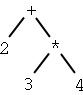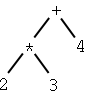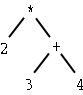KOI: Postfix notation
The same expression can be written in several different ways:
-
The usual notation, such as x + 3, is called infix.
The operator (+) is placed between the operands (x and 3).
-
In prefix notation, you put the operator before the operands.
For unary operators and functions, this is the normal notation: -x, sin(x).
-
In postfix notation, you put the operator after the operands.
Some examples:
| Tree | Infix notation | Prefix notation | Postfix notation |
|---|
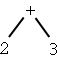
|
2 + 3
|
+ 2 3
|
2 3 +
|
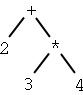
|
2 + 3 * 4
|
+ 2 * 3 4
|
2 3 4 * +
|
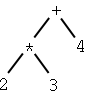
|
2 * 3 + 4
|
+ * 2 3 4
|
2 3 * 4 +
|
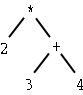
|
2 * (3 + 4)
|
* 2 + 3 4
|
2 3 4 + *
|
If you are writing a program that calculates the values of expressions,
the program must be more complicated to understand the usual infix notation,
than if you use prefix or postfix notation.
The reason is that with infix notation,
the program must take operator precedence into account.
Operator precedence is also called operator priority.
Multiplication has higher precedence than addition,
which means that if an expression contains both a multiplication and an addition,
the multiplication should be performed first.
Look at 2 + 3 * 4 and 2 * 3 + 4 in the table!
Postfix notation is simpler.
First, you need a stack, where you can put numbers.
To calculate the value of a postfix expression,
then look at each operand or operator in turn,
from left to right, and do this:
-
If it is a number, then put it on top of the stack.
-
If it is an operator, then take the two numbers on top of the stack,
apply the operator to them,
and put the result back on top of the stack.
As an example, look at how the stack changes when we
calculate the postfix expression 2 3 * 4 +:
| Start | 2 | 3 | * | 4 | + |
|---|
|
|
2
|
3
2
|
6
|
4
6
|
10
|
Replay!
And again! (So, which one looks best?)
Thomas Padron-McCarthy
(Thomas.Padron-McCarthy@tech.oru.se)
August 20, 2007