Ett datorspråk är ett språk som är skapat för att läsas och förstås av datorer. Det kan vara ett programmeringsspråk som C++, Java eller Visual Basic, men det kan också vara ett betydligt enklare språk, som till exempel beskriver vad man kan skriva i en konfigurationsfil, eller vad man kan mata in i en inmatningsruta.
En grammatik för ett språk beskriver språket, och talar om hur man kan sätta samman meningar och andra konstruktioner i det språket.
Det finns också naturliga språk som svenska och engelska. De naturliga språken brukar vara mycket friare än datorspråken, så att man till exempel kan vända på ordföljden. Gränsen mellan rätt och fel brukar också vara lite flytande i de naturliga språken.
Eftersom datorer är mycket dummare än människor, måste man vara mycket mer noggrann när man skriver något som en dator ska läsa och förstå. En människa kan ofta förstå en mening trots att det, finns ett kommatecken på fel ställe. Men om man skriver ett kommatecken på fel ställe i ett program, så kommer datorn för det mesta att göra antingen inget alls, eller något helt annat än vad man tänkt sig.
Grammatiken för språket svenska säger till exempel att man kan skapa en mening bland annat genom att först skriva ett substantiv och sen ett verb, och avsluta med en punkt. Den regeln skulle man kunna skriva så här:
mening -> substantiv verb .
Man kan alltså ta ett substantiv, vilket som helst, följt av ett verb, vilket som helst, och en punkt, och detta bildar en mening.
Eftersom naturliga språk som svenska är ganska fria, är det svårt eller omöjligt att skriva en fullständig och korrekt grammatik, som verkligen beskriver allt man kan säga på svenska.
Det är mycket lättare att skriva en grammatik för ett datorspråk. Dels brukar datorspråk vara mycket enklare än naturliga språk, och dessutom är de mycket mer exakt bestämda. Det finns inga (nåja, nästan inga) tveksamma fall, utan om man skriver något i ett datorspråk som Java så är det antingen rätt eller fel. Inte som i svenska, där man kan diskutera ganska länge om ett uttryck är rätt eller fel, och där det i slutänden kanske visar sig vara en smaksak.
En hälsning kan alltså vara antingen god morgon, god middag eller god kväll. Symbolen "|" betyder "eller". Symbolen "->" kan läsa som "kan ersättas med" eller "kan expanderas till".hälsning -> hej | god morgon | god middag | god kväll
Det här är en annan grammatik, som beskriver precis samma språk:
En hälsning är alltså ordet god, följt av en tidsspecifikation, och den tidsspecifikationen kan vara antingen morgon, middag eller kväll.hälsning -> hej | god tidsspecifikation tidsspecifikation -> morgon | middag | kväll
I stället för att använda eller-tecknet "|" för att visa att en tidsspecifikation kan vara någon av flera olika saker, kan man skriva flera olika regler:
hälsning -> hej hälsning -> god tidsspecifikation tidsspecifikation -> morgon tidsspecifikation -> middag tidsspecifikation -> kväll
I grammatiken använder vi också namnen hälsning och tidsspecifikation. De förekommer inte i hälsningsspråket, utan finns bara i grammatiken. De kallas icke-terminaler, och vi skriver dem med kursiv stil.
En "terminal" är något som finns på slutet av något. På slutet av en busslinje finns en bussterminal. Där stannar bussen, och busspassagerarna kliver av. Om jag har en icke-terminal, som hälsning, så kan jag fortsätta och ersätta den, enligt reglerna i grammatiken, men när jag kommit till en terminal, som morgon, så kan jag inte ersätta den med något annat, utan jag måste stanna där.
En produktion är en regel i grammatiken, som säger att en viss icke-terminal kan ersättas med något annat. Till exempel är det här en produktion som säger att icke-terminalen hälsning kan ersättas med terminalen god och icke-terminalen tidsspecifikation:
Notera också att det här inte är en produktion, utan tre:hälsning -> god tidsspecifikation
"Eller"-tecknet "|" är bara ett kortare sätt att skriva flera olika produktioner, och i stället för det ovanstående kan man skriva ut dem:tidsspecifikation -> morgon | middag | kväll
tidsspecifikation -> morgon tidsspecifikation -> middag tidsspecifikation -> kväll
Jo, när man skriver en grammatik räcker det inte med att ange vilka terminaler, icke-terminaler och produktioner som finns, utan man måste också ange vad det egentligen är för saker man vill säga i språket, om det till exempel är hela hälsningar eller bara tidsspecifikationer. Det gör man genom att ange en startsymbol.
För vårt hälsningsspråk är det hälsning som är startsymbol, inte tidsspecifikation.
När vi i fortsättningen talar om ett språk, så menar vi mängden av alla tillåtna sekvenser av terminaler. Det här enkla språket innehåller fyra tillåtna sekvenser, men ett språk som C++ innehåller förstås många fler - kanske till och med oändligt många.
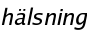
Det finns två olika sätt att expandera den:
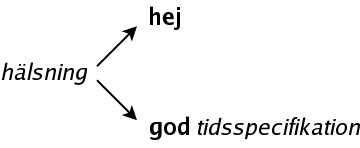
hej kan inte expanderas, så där kommer vi inte vidare, men icke-terminalen tidsspecifikation kan expanderas på tre olika sätt:
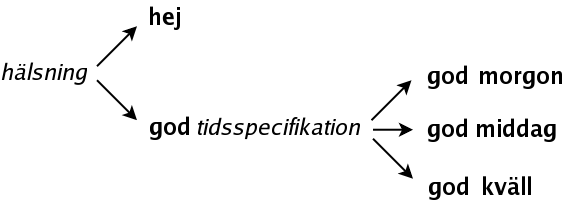
Nu kommer vi inte längre.
Vi har bildat ett träd, och språket, dvs vilka sekvenser av terminaler som är tillåtna, hittar vi genom att titta på löven i trädet.
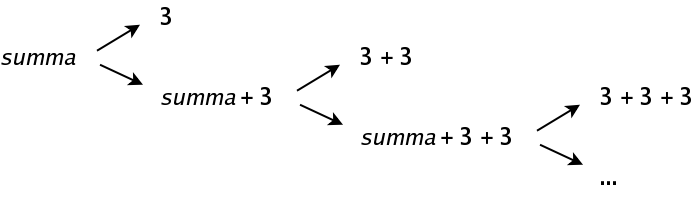
Trots att språket bara har två terminaler, två produktioner och en icke-terminal, innehåller det oändligt många tillåtna sekvenser:
Det finns flera sätt att skriva en sån här grammatik, men vi väljer att tänka så här: En summa är antingen en ensam siffra, eller så har man en summa (som kan vara en ensam siffra) där man adderar en ny siffra på slutet, så att det blir en ny summa.
Ett första försök:
Då blir grammatiken ännu enklare:
Nu syns det kanske lite tydligare hur vi tänkte: En summa är antingen en ensam siffra, eller så har man en summa (som kan vara en ensam siffra) där man adderar en ny siffra på slutet, så att det blir en ny summa.
Källprogrammet som ska kompileras består normalt av text, dvs en följd av tecken:
x = y + 14;Scannern läser källprogrammets text, och skapar i stället en sekvens av terminaler, eller "tokens", som skickas vidare till parsern:
identifierare, likhetstecken, identifierare, plustecken, heltal, semikolonNormalt skickar scannern också med information om vilka identifierare och heltal som den hittade, så här nånting:
identifierare (x), likhetstecken, identifierare (y), plustecken, heltal (14), semikolonParsern läser denna sekvens av tokens, jämför med grammatiken, och avgör om det är en tillåten sekvens av tokens enligt grammatiken, och vilka av produktionerna i grammatiken som behövs för att generera denna sekvens.
När man konstruerar en kompilator kan man ibland välja om man vill placera en viss del av arbetet i scannern eller i parsern. Till exempel såg vi ju här ovan att man kunde låta parsern ha en regel för att en "siffra" är någon av 0 till 9, eller så kunde man låta scannern sköta om att känna igen att 0 till 9 är siffror.
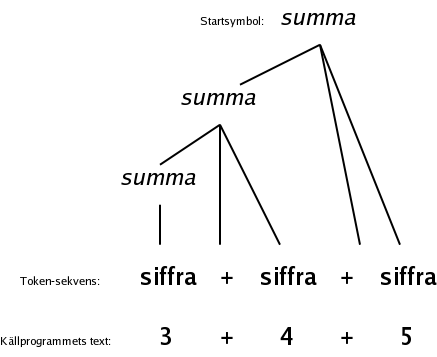
Fast det där var inte riktigt sant. Det är inte säkert att parsern bygger upp något parse-träd, och i de fall den gör det brukar man räkna själva byggandet till nästa fas i kompilatorn, nämligen "generering av mellankod". I stället är det så att parsern går igenom produktionerna i grammatiken i en ordning så att den skulle kunna bygga upp ett parse-träd.
Man kan förenkla parse-trädet genom att (1) ta bort de inre noder som bara har en under-nod, och (2) flytta upp operatorer till noden ovanför, där de ersätter icke-terminalen:
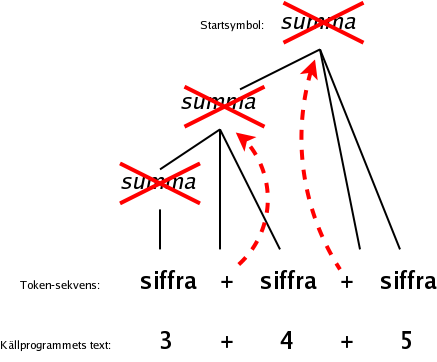
Då bildas ett så kallat syntax-träd, ibland också kallat abstrakt syntax-träd:
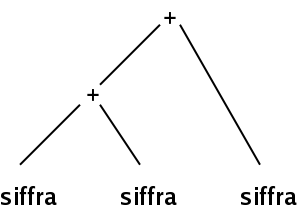
Det enklare syntaxträdet innehåller all information som behövs för att beräkna uttrycket (eller köra programmet), men har inte med den information om grammatikens struktur som fanns i parse-trädet.
Ett annat sätt att tänka är detta: En summa är antingen en ensam siffra, eller två summor som man adderar:
Att en grammatik är tvetydig betyder att samma sekvens av tokens kan beskrivas med (minst) två olika parse-träd, enligt den grammatiken. Nottera hur 3+4+5 kan beskrivas på två sätt:
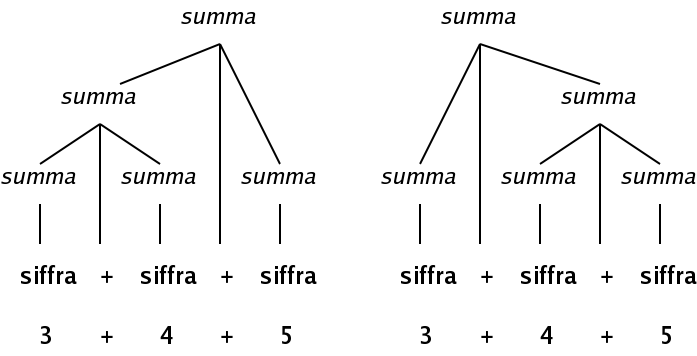
Om man grupperar additionerna med parenteser, motsvarar detta de två uttrycken (3+4)+5 respektive 3+(4+5).
Man kan förstå undra om det spelar någon roll, och för addition gör det inte det. Bägge summorna ger resultatet 12, och en addition ger alltid samma resultat oavsett i vilken ordning man adderar termerna. Men om vi i stället för addition haft subtraktion, så hade de två uttrycken blivit (3-4)-5 respektive 3-(4-5). De ger helt olika resultat.
Motsatsen till en tvetydig grammatik är en entydig grammatik. En grammatik för ett datorspråk bör vara entydig, för en tvetydig grammatik gör ju att ett källprogram kan tolkas på olika sätt, och det är svårt för datorn att med någon sorts "sunt förnuft" veta vilken av de olika tolkningarna som är den avsedda.
Ett första försök att skriva grammatiken:
Det där är en tvetydig grammatik (prova själv!). Nästa försök:
Det är bättre, men den klarar bara uttryck på formen tal * tal + tal * tal.
Vi vill kunna multiplicera ihop godtyckligt många tal till en term, och addera ihop godtyckligt många termer till ett uttryck. Då måste både term-regeln och uttrycks-regeln hantera det. Vi använder det vi lärde oss tidigare om hur man kan kedja ihop summor genom att hela tiden lägga till + siffra till en summa.