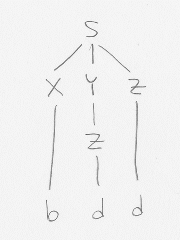
så innehåller följande programrader fel som kan upptäckas i den lexikaliska, syntaktiska respektive semantiska analysen:float f; char* s;
f = 3.14e19e17; f f; f = s;
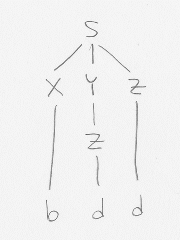
b) (3p)
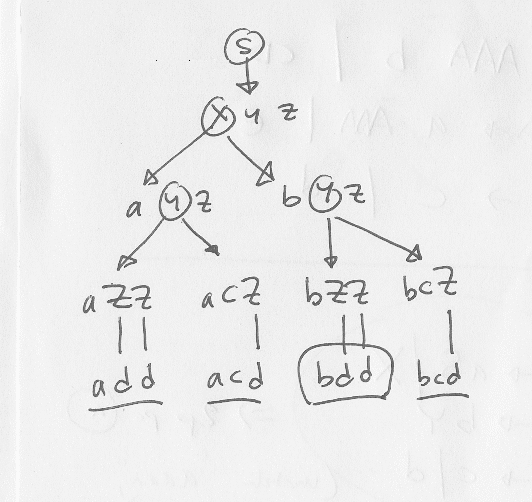
add, acd och bcd
Man kan hitta dem genom att börja med startsymbolen, och sen systematiskt tillämpa alla reglerna i grammatiken:
c) (1p)
Att två eller flera olika parse-träd kan byggas från samma tokensekvens. (Annorlunda uttryckt: Att ingen tillåten tokensekvens kan härledas ur mer än ett parse-träd.)
d) (2p)
Nej, den är inte tvetydig, för ingen av de tillåtna tokensekvenserna kan härledas ur mer än ett parse-träd.
e) (2p)
Exempelvis [ab][cd]d
f) (2p)
Ja, till exempel {add,acd,bdd,bcd} eller {a,b}{c,d}d eller {ac,ad,bc,bd}d
Vänsterrekursion innebär att en produktions vänsterled återkommer som det första elementet i högerledet, exempelvis som i produktionen
S -> S x
b) (2p)
Antag att grammatiken ser ut så här:
A är en icke-terminal, men x och y kan stå för godtyckliga konstruktioner, med flera terminaler och icke-terminaler.A -> A x | y
Regeln ersätts av följande två regler, som beskriver samma språk men som inte är vänsterrekursiva:
A -> y R R -> x R | empty
Exempel: Den här vänsterrekursiva grammatiken,
kan skrivas om till denna, som inte är vänsterrekursiv:uttryck -> uttryck + term | term
I det här exemplet motsvarades A, x, y och R alltså av:uttryck -> term rest rest -> + term rest | empty
c) (1p)
Inte alls. Språket (dvs mängden av alla tillåtna tokensekvenser) är fortfarnade samma.
d) (2p)
När man ska bygga en prediktiv recursive-descent-parser. Annars kommer parsern att fastna och "stå och stampa" på den regeln. Antag att den hittar en token som kan inleda en tokensekvens som motsvarar icke-terminalen S i regeln S -> S x. Då expanderar den S till S x, varpå den fortfarande står vid samma token i inmatningen. Denna token kan förstås fortfarande inleda en tokensekvens som motsvarar icke-terminalen S, så den expanderar (igen) S till S x, utan att ha förbrukat någon token i inmatningen. Och så håller det på.
e) (2p)
Man betraktar de semantiska aktionerna som vilka element i grammatiken som helst, och flyttar runt dem på samma sätt som terminalerna och icke-terminalerna. (Om de innehåller $-referenser i Yacc kan dessa behöva numreras om.)
Exempel: Den här vänsterrekursiva grammatiken,
uttryck -> uttryck + term { print("+") } | term
kan skrivas om till denna, som inte är vänsterrekursiv:
uttryck -> term rest
rest -> + term { print("+") } rest | empty
I det här exemplet motsvarades A, x, y och R alltså av:
S -> AAA b | CD AAA -> a A | empty CD -> c | d
S är startsymbol.
b) (7 p)
void error() {
printf("Ledsen error.\n");
exit(EXIT_FAILURE);
}
void match(int expected) {
if (lookahead != expected)
error();
else
lookahead = scan();
}
extern void S(), AAA(), CD();
void S() {
printf("S\n");
AAA(); match('b'); CD();
}
void AAA() {
printf("AAA\n");
if (lookahead == 'a') {
match('a'); AAA();
}
else {
/* Matchar empty, dvs nästa token kan vara vad som helst */
}
}
void CD() {
printf("CD\n");
if (lookahead == 'c') {
match('c');
}
else if (lookahead == 'd') {
match('d');
}
else {
error();
}
}
void parse() {
printf("parse\n");
lookahead = scan();
S();
match('$'); /* Slutet på indata antas markeras med '$' */
printf("Ok.\n");
}
Matchningen mot $, som vi antar markerar slutet på tokensekvensen i indata, behövs bara om det inte får komma mer data efter det som matchas av grammatiken.
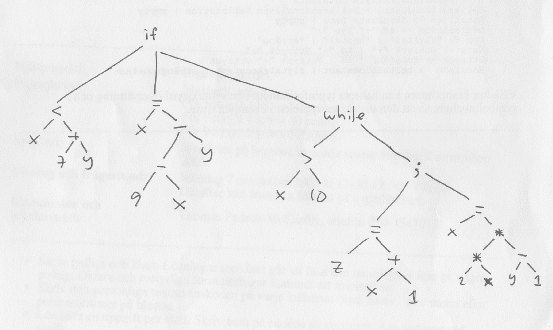
b) (3p) postfixkod för en stackmaskin
rvalue x (inte lvalue!)
push 7
rvalue y
+
<
gofalse 1
lvalue x
push 9
rvalue x
-
rvalue y
-
=
goto 2
label 1:
label 3:
rvalue x (inte lvalue!)
push 10
>
gofalse 4
lvalue z
rvalue x
push 1
+
=
lvalue x
push 2
rvalue x
*
rvalue y
push 1
-
*
=
goto 3
label 4:
label 2:
c) (4p) treadresskod
temp1 = 7 + y;
if (x >= temp1) goto 1;
temp2 = 9 - x;
temp3 = temp2 - y;
x = temp3;
goto 2;
label 1:
label 3:
if (x <= 10) goto label 4;
temp4 = x + 1;
z = temp4;
temp5 = 2 * x;
temp6 = y - 1;
temp7 = temp5 * temp6;
x = temp7;
goto 3;
label 4:
label 2:
Den innehåller lagringsutrymme för procedurens formella parametrar, dess lokala variabler, och temporärvariabler som används i proceduren. Den innehåller också plats för att lagra återhoppsadress och returnerat funktionsvärde. (Flera av alla dessa saker lagras ofta i stället i register.) Dessutom kan maskinstatus från den anropande funktionens exekvering, främst innehållet i processorns register, sparas undan i aktiveringsposten.
Det kan också finnas en "dynamisk länk" eller "kontrollänk" till aktiveringsposten för den procedur som anropade den här proceduren, och en "statisk länk" eller "åtkomstlänk" till en aktiveringspost för den procedur som närmast omsluter den här proceduren i programkoden.
För "vanliga" språk som C, C++, Java och Pascal placeras aktiveringsposten på stacken. (En aktiveringspost per anrop till varje procedur.) För språk med enbart statisk allokering, som uråldriga versioner av FORTRAN, är aktiveringsposten för varje procedur statiskt allokerad. (Endast en aktiveringspost per procedur.) Man kan också allokera aktiveringsposterna på heapen, till exempel i språk där man kan avbryta och återstarta exekveringen av en procedur.
Varje variabel får en post i symboltabellen, där det också lagras vilken typ den tillhör. Dessa data läggs in när kompilatorn hittar variabeldefinitionerna i källprogrammet.
| Id | Lexem | Typ | ... |
|---|---|---|---|
| 1 | s | sträng | |
| 2 | i | heltal | |
| 3 | foo | flyttal | |
| 4 | fum | sträng |
Varje konstant och variabel som sen används i källprogrammet har en typ. För variablerna hämtas typen ur symboltabellen. När variabler och konstanter kombineras i uttryck, dvs i tilldelningar och additioner, utgår man från dessa typer, och kontrollerar om de typkombinationerna är tillåtna för den aktuella operationen.
Man kan lägga in semantiska aktioner i grammatiken, som håller reda på typinformation för varje uttryck, och kontrollerar att det inte blir några konflikter (som att ett uttryck med typen heltal ska läggas i en variabel med typen sträng).
Vi kan tänka oss att det finns två subrutiner: spara som lägger till en typ till en variabel lagrad i symboltabellen, och hämta som returnerar en symboltabellpost för en variabel. Den posten innehåller bland annat ett typfält, typ.
Grammatiken behöver nu kompletteras med de semantiska aktionerna för typ-propagering och typkontroll, till exempel så här (men alla dessa behöver inte vara med för full poäng på uppgiften, utan det räcker med ett antal belysande exempel):
S -> Deklarationslista Satslista
{
if (Deklarationslista.typ == void && Satslista.typ == void)
S.typ = void;
else
S.typ = typfel;
}
Deklarationslista -> Deklarationslista1 Deklaration
{
if (Deklarationslista1.typ == void && Deklaration.typ == void)
Deklarationslista.typ = void;
else
Deklarationslista.typ = typfel;
}
Deklarationslista -> empty { Deklarationslista.typ = void; }
Satslista -> Satslista Sats
{
if (Satslista1.typ == void && Sats.typ == void)
Satslista.typ = void;
else
Satslista.typ = typfel;
}
Satslista -> empty { Satslista.typ = void; }
Deklaration -> id ":" Typ ";"
{
spara(id.tokenval, Typ.typ);
Deklaration.typ = void;
}
Typ -> "flyttal" { Typ.typ = flyttal; }
Typ -> "heltal" { Typ.typ = heltal; }
Typ -> "sträng" { Typ.typ = sträng; }
Sats -> Uttryck ";"
{
if (Uttryck.typ == typfel)
Sats.typ = typfel;
else
Sats.typ = void;
}
Sats -> id "=" Uttryck ";"
{
if (hämta(id.tokenval).typ == typfel || Uttryck.typ == typfel)
Sats.typ = typfel;
else if (hämta(id.tokenval).typ == Uttryck.typ)
Sats.typ = void;
}
Uttryck -> Konstant { Uttryck.typ = Konstant.typ; }
Uttryck -> id { Uttryck.typ = hämta(id.tokenval).typ; }
Uttryck -> Uttryck1 "+" Uttryck2
{
// Ja, det här villkoret kan förenklas
if (Uttryck1.typ == typfel || Uttryck2.typ == typfel)
Uttryck.typ = typfel;
else if (Uttryck1.typ == sträng || Uttryck2.typ == sträng)
Uttryck.typ = typfel;
else if (Uttryck1.typ == Uttryck2.typ)
Uttryck.typ = Uttryck1.typ;
else
Uttryck.typ = typfel;
}
Konstant -> heltalskonstant { Konstant.typ = heltal; }
Konstant -> flytalskonstant { Konstant.typ = flyttal; }
Konstant -> strängkonstant { Konstant.typ = sträng; }