
Today:
Optimization.
ASU chapter 10. (KP chapter 6.)
"Hand optimization", example:
for (i = 0; i < n; ++i) {
do_something(a[i]);
}
Equivalent to:
i = 0;
while (i < n) {
do_something(a[i]);
++i;
}
Can be "optimized" to:
p = &a[0];
p_after = &a[n];
while (p != p_after) {
do_something(*p);
++p;
}
Probably no effect, or even slower. Better handled by the compiler!
Two rules about optimization by hand:
Types of optimization:
Peep-hole optimization (ASU 9.9): Simple transformations of the generated assembly (or machine) code. Ex:
| can be changed to |
|
void quicksort(int m, int n) {
int i, j;
int v, x;
if (n <= m)
return;
i = m-1; j = n; v = a[n];
while (1) {
do
i = i + 1;
while (v > a[i]);
do
j = j - 1;
while (a[j] > v);
if (i>=j)
break;
}
x = a[i]; a[i] = a[n]; a[j] = x;
quicksort(m, j);
quicksort(i+1, n);
}
Some optimizations are not possible on the source level.
ASU fig. 10.4, three-address code for a part of the quicksort function:

Steps for the optimizer:
ASU fig. 10.5, basic blocks and flow graph for the quicksort function:
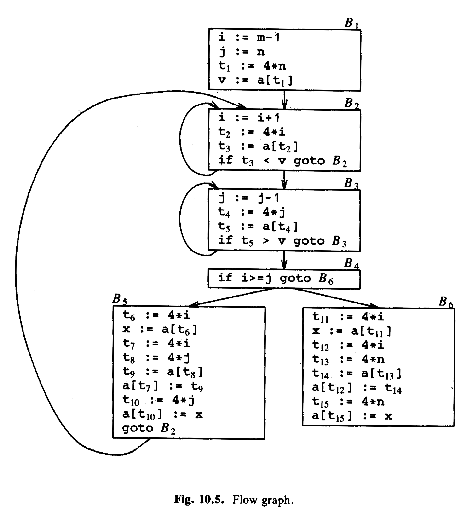
Three loops:
B5:
| can be changed to |
|
(Remove repeat calculations, use t6 instead of t7, t8 instead of t10.)
From fig 10.5/10.6:
(We can remove 4*i, 4*j, and 4*n completely from B6!)
Remove 4*i and 4*j completely from B5!
B5:
| can be changed to |
|
| can then be changed to |
|
Note: a hasn't changed, so a[t4] still in t5 from B3
| can then be changed to |
|
ASU fig. 10.7, after eliminating (global) common subexpressions:
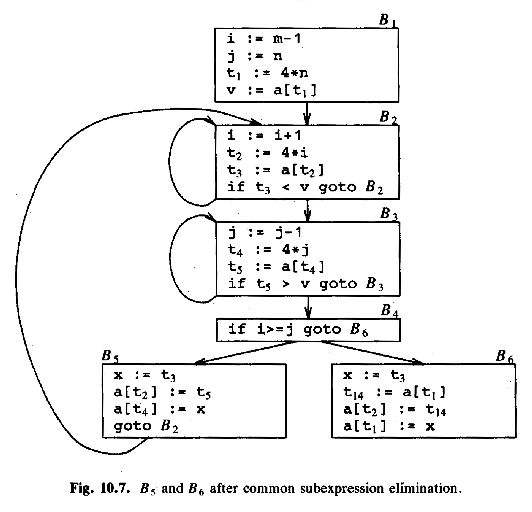
B5:
| can be changed to |
|
B5:
| but x is dead, so: |
|
The expressions limit - 2 and x + y are loop-invariant.while (i < limit - 2) a[i] = x + y;
The next example is harder for the compiler, since strlen is just another function. (Or is it?)t1 = limit - 2; t2 = x + y; while (i < t) a[i] = t2;
for (i = 0; i < strlen(s1); ++i) s2[i] = s1[i];
n = strlen(s1); for (i = 0; i < n; ++i) s2[i] = s1[i];
i = 0;
j = 1;
while (a1[i] != 0) {
a2[j] = a1[i];
++i;
++j;
}
Both i and j are induction variables ("loop counters").
i = 0;
while (a1[i] != 0) {
a2[i + 1] = a1[i];
++i;
}
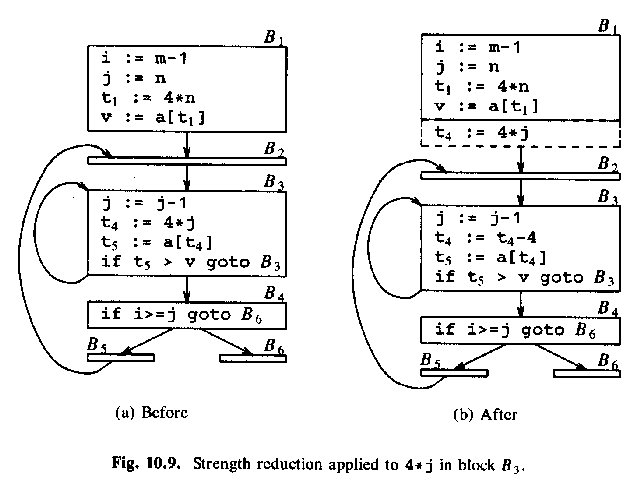
Then a similar strength reduction of 4 * i in basic block B2.
We know that t2 == 4 * i. Maintain this relationship!
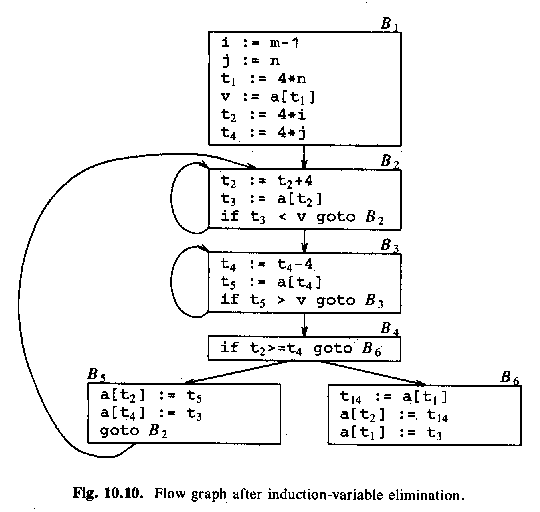
Then, i and j are used only in the test int B4.
The test
i >= j
can be changed to
4 * t2 >= 4 * t4
(which is equivalent to
t2 >= t4).
i and j become dead!
ASU fig 10.10, after eliminating induction variables i and j:
for (i = 0; i < 20; ++i)
for (j = 0; j < 2; ++j)
a[i][j] = i + 2 * j;
may be transformed by unrolling the inner loop:
for (i = 0; i < 20; ++i) {
a[i][0] = i;
a[i][1] = i + 2;
}
int a;
...
void f(string a) {
...
while (1) {
int a;
... <-- In the debugger: print a
}
}
What is needed, for symbolic debugging in general?
A program may work when unoptimized, but not when optimized. For example, the C standard specifies undefined behaviour in certain cases. such as:
The behaviour depends entirely on what happens to be stored at the memory location 5 bytes after the end of s: unused padding, a variable, or the return address in an activation record? This can be different with or without optimization, since optimization, for example, can eliminate variables.char s[10]; ... s[14] = 'x';
ASU fig 10.68. Assume that the source, intermediate and target representation are the same.

ASU fig 10.69. A DAG for the variables. The DAG shows how values depend on each other. Then, annotate it with life-time information.
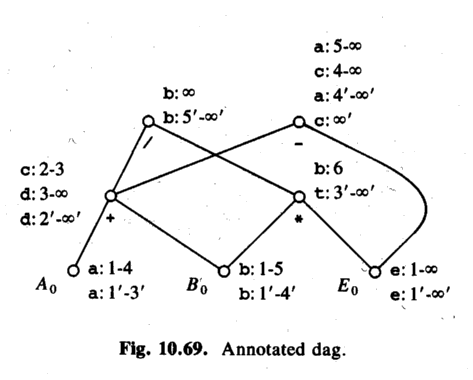
Example 1 (just the unoptimized program):
c = a + b after step 1. (Life time: 2-3)
c = c - e after step 3. (Life time: 4-infinity)
Example 2 (the optimized program):
c = a after step 5'. (Life time: 6'-infinty)
c is undefined in 1'-5'!
(But can be calculated, differently depending on when!)
Example 3:
An overflow occurs in the optimized code, in statement 2',
t = b * e.
The first source statement that uses the node b * e is 5.
Therefore, tell the user the program crashed in source statement 5!
Then the user says:
print b -> show b (lifetime 1-5 and 1'-4')
Explanation: b still has its initial value, both at 2' and at 5.
print c -> can't show actual stored c (lifetime 6-infinity)
Instead, find the DAG node for c at time 5 (-).
(Optimized) a will contain this value after 4', but not yet!
Consider the children:
d contains the value from the + node at 2'-infinity.
e contains the value from the E0 node at 1'-infinity.
So use d - e!