Kompilatorer och interpretatorer: Lecture 11

Note: This is an outline of what I intend to say on the lecture. It is not a definition of the course content, and it does not replace the textbook.

Today:
Some rests from lecture 10 about type checking (ASU 6.1-6.3).
Intermediate code generation.
ASU 8.1-8.3. KP chapter 5.

Rest from the previous lecture: Type checking

6.2 Specification of a simple type checker

...

Type checking of functions

Grammar for function call:
Expr --> Expr1 ( Expr2 )
Add function declarations to the declaration part, for example with the type syntax int -> int:
f : int -> int;
f(7) + 3;
Grammar for the function type:
Type --> Type1 "->" Type2
Translation scheme for the function type: 
Type --> Type1 "->" Type2
  { Type.type = function(Type1.type, Type2.type); }
Translation scheme for type checking a function call: 
Expr --> Expr1 ( Expr2 )
  { if (Expr1.type == function(s, t) and Expr2.type == s)
      Expr.type == t;
    else
      Expr.type == type_error;
  }

6.3 Equivalence of type expressions

Learn the difference between: Structural equivalence in C: 
typedef int T1;
typedef int T2;

T1 t1;
T2 t2;

t1 = t2; // ok
More structural equivalence in C -- m1 and m2 have the same type: 
double m1[14][17];
double m2[14][17];
Checking type equivalence:

C uses structural equivalence for all types except records ("structs"): 

struct A { int foo; double fum; };
struct B { int blaj; double urko; };

struct A a;
struct B b;

a = b; // "incompatible types in assignment"
This is to aviod cycles in the type representation: 
struct L {
  int foo;
  struct L* next;
};
But note that TA1 and TA2 are the same type (since both are A): 
typedef struct A TA1;
typedef struct A TA2;

TA1 ta1;
TA2 ta2;

ta1 = ta2; // ok

8. Intermediate code generation

Why not do everything "in the Yacc grammar"? Some reasons:

8.1 Intermediate languages

Some ways to represent the program:

Graphical representations: Trees (or DAGs)

As before. Just note two things more: ASU Fig 8.4:

Two representations of a tree

Three-Address Code

var1 = var2 operation var3

Example: x + y * z 

temp1 = y * z
temp2 = x + temp2
Note: Example (on rearranging): (a - b) - (a + b)

Postfix: a b - a b + -

Three-Address code: 

temp1 = a - b
temp2 = a + b
temp3 = temp1 - temp2
Idea: Each internal node corresponds to a temp-variable!

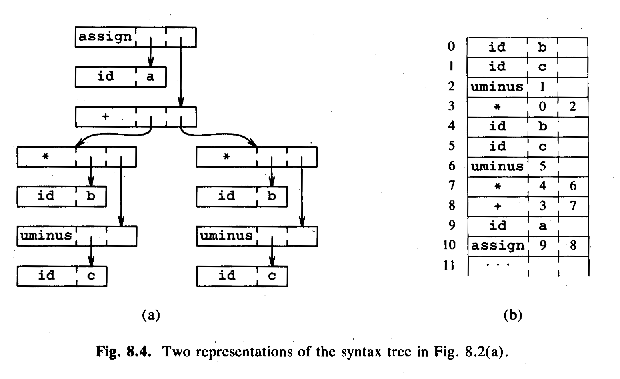
Example: a = b * -c + b * -c (The tree in Fig. 8.4a) 

temp1 = - c
temp2 = b * temp1
temp3 = - c
temp4 = b * temp1
temp5 = temp2 + temp4
a = temp5
The DAG in Fig. 8.4b: 
temp1 = - c
temp2 = b * temp1
temp5 = temp2 + temp4
a = temp5

Types of three-address statements

  1. Assignment: x = y op z (Ex: temp5 = a + temp4)
  2. Assignment: x = op y (Ex: temp3 = - temp4)
  3. Copy: x = y (Ex: a = temp3)
  4. Jump: goto L
  5. Conditional jump: if x relop y goto L (Ex: if (temp7 < temp2) goto L7)
  6. Procedure call: call p, n
  7. Parameter for procedure call: param x
  8. Return from procedure call: return y. Ex: 
    param temp4
param a
param b
call f, 3
  9. Indexed assignment: x = y[z] (ex: temp5 [ temp4 ] = temp9)
  10. Indexed assignment: x[y] = z
  11. Pointer and address operations: x = &y
  12. x = *y
  13. *x = y

Syntax-directed translation into three-address code

Synthesized attributes:
E.place = the name of the temporary variable
E.code = the sequence of three-address statements that calculates the value (or they could be written to a file instead of stored in the attribute)

Production Semantic rule
Start -> id = Expr Start.code = Expr.code + { id.place ":=" Expr.place }
Expr -> Expr1 + Expr1 Expr.place = make_new_temp();
Expr.code = Expr1.code + Expr2.code + { Expr.place = Expr1.place "+" Expr2.place; }
Expr -> Expr1 * Expr1 Expr.place = make_new_temp();
Expr.code = Expr1.code + Expr2.code + { Expr.place = Expr1.place "*" Expr2.place; }
Expr -> - Expr1 Expr.place = make_new_temp();
Expr.code = Expr1.code + { Expr.place = "-" Expr1.place; }
Expr -> ( Expr1 ) Expr.place = Expr1.place; // No new temp!
Expr.code = Expr1.code;
Expr -> id Expr.place = id.place; // No temp!
Expr.code = ' '; // No code!

While statement (very similar to generating stack machine code, see lecture 9);

Production Semantic rule
Stmt -> while ( Expr ) Stmt1 Stmt.before = make_new_label();
Stmt.after = make_new_label();
Stmt.code = { "label" Stmt.before } + Expr.code +
{ "if" Expr.place "==" "0" "goto" Stmt1.after; } +
Stmt1.code +
{ "goto" Stmt.before } + { "label" Stmt.after };

Quadruples

A way to represent three-address code.

Op Arg1 Arg2 result
0 uminus c temp1
1 * b temp1 temp2
2 uminus c temp3
3 * b temp3 temp4
4 + temp2 temp4 temp5
5 := temp5 a

Skip: Also "triples" (but they are hard to optimize) and "indirect triples" (as easy to optimize as quadruples, but more complicated).

8.2 Declarations

Declarations in a procedure

Keeping track of scope information

ASU Fig 8.12:

Symbol tables for nested procedures

Fields names in records

8.3 Assignment statements

Names in the symbol table

Reusing temporary names

Addressing array elements

The translation scheme for addressing array elements

ASU Fig 8.18:

Annotated parse tree for x := A[y, z]

Type conversions withing assignments

Accessing fields in records

Thomas Padron-McCarthy (Thomas.Padron-McCarthy@tech.oru.se) February 26, 2004