Today:
Parsing by hand, the simple compiler program
Aho et al, sections 2.4 - 2.7, 2.9
But first: Rest from lecture 2:
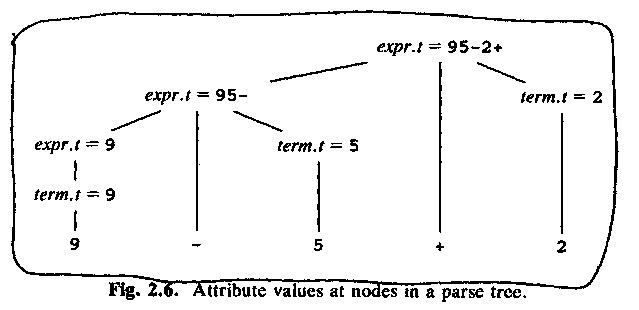
Syntax-directed definition = context-free grammar, plus a semantic rule (Sw: semantisk regel) for each production, that specifies how to calculate values of attributes. Example:
| Production | Semantic rule |
|---|---|
| expr -> expr1 + term1 | expr.output -> expr1.output + term1.output + " +" |
ASU fig 2.6, an annotated (= with attribute values) parse tree:

A syntax-directed definition says nothing about how the parser should build the parse tree! Just the grammar, and what to do when the tree is finished.
Syntax-directed definition = context-free grammar, plus semantic actions (Sw: semantiska aktioner, semantiska åtgärder) for each production, that specifies what to do. Example:
expr -> expr1 + term1 { print("+"); }
Generates postfix!
Or, with the action somewhere in the middle:
rest -> + term1 { print("+"); } rest1
The semantic actions are put in the parse tree, just like the "real" parts. ASU fig 2.12:
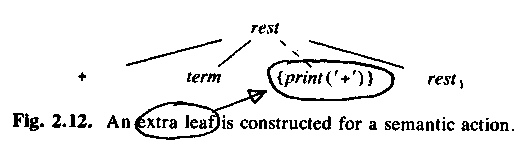
ASU fig 2.14: 9-5+2, with semantic ations
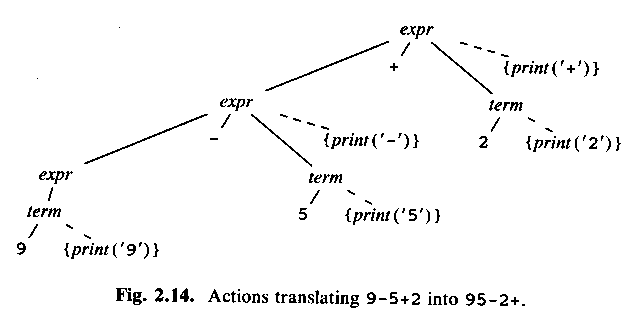
As with a syntax-directed definition, a syntax-directed scheme says nothing about how the parser should build the parse tree! Just the grammar, and what to do when the tree is finished.
But we don't actually have to build the tree. Just perform the semantic actions as the tree is (not) built!
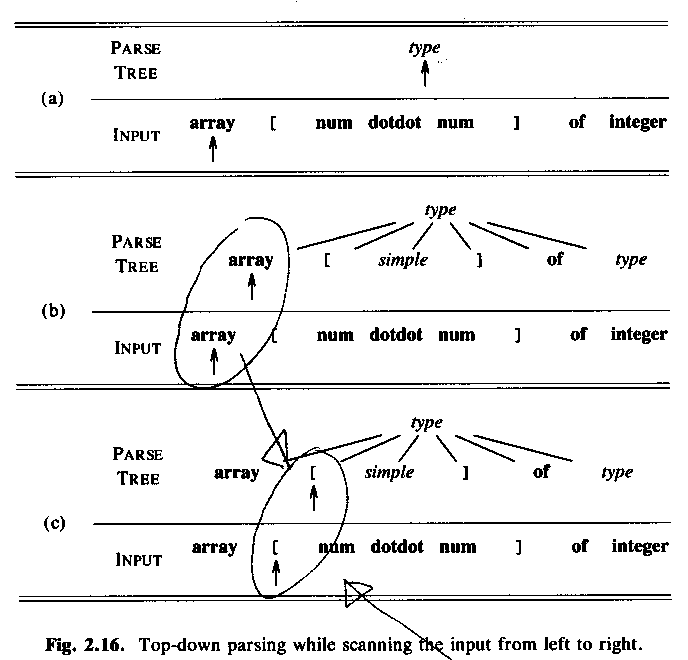
Examples:simple -> integer simple -> char simple -> num dotdot num type -> simple type -> ^ id type -> array [ simple ] of type
Example source program:integer 1..100 ^kundpost array [ integer ] of char array [ 20..40 ] of 0..3 array [ 1..5 ] of array [ 1..3 ] of 2..5
Tokens:
array [ num dotdot num ] of integer
Top-down parsing, starting with a node for the non-terminal type.
Which of the productions (=rules) should we use? (Answer: type -> array ....)
Why? (Answer: The only production that starts with array.)
"Lookahead symbol" = "current token" = Sw: "aktuell token"
ASU fig 2.15:
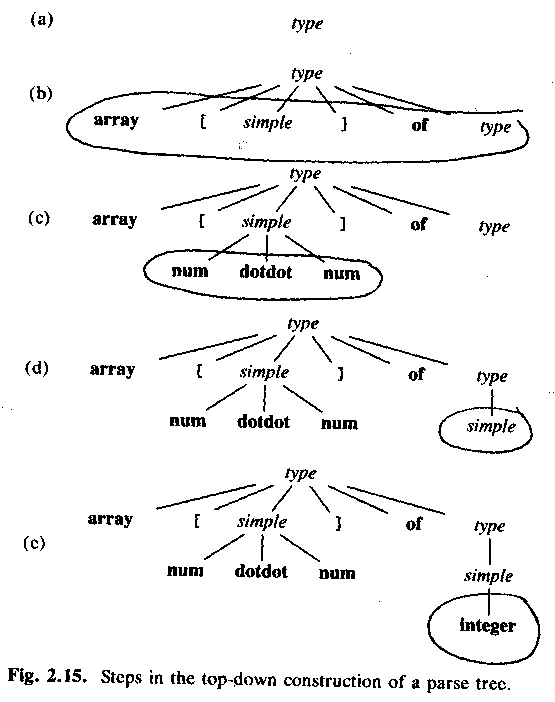
ASU fig 2.16:
If always just one production possible to chose: predictive parsing, no backtracking
void type() {
if (lookahead == integer or lookahead == char or lookahead == num)
simple();
else if (lookahead == ^) {
match(^); match(id);
}
else if (lookahead == array) {
match(array); match([); simple(); match(]); match(of); type();
}
else
error();
}
match() checks that the lookahead symbol (=current token) is the expected one,
and gets the next token (typically by calling the lexical analyzer).
void simple() {
if (lookahead == integer)
match(integer);
else if (lookahead == char)
match(char);
else if (lookahead == num) {
match(num); match(dotdot); match(num);
}
else
error();
}
When we write type(),
it is not enough to see which tokens occur as the first token
in the productions for type (^ and array).
Since simple can occur as the first thing in a type,
we must also see which tokens occur as the first token in productions for simple.
FIRST(x) = all possible first tokens in strings that match x.
FIRST(simple) = the set { integer, id, char }
FIRST(^ id) = the set { ^ }
FIRST(array [ simple ] of type) = the set { array }
FIRST(type)
= the set { ^, array } + the set FIRST(simple)
= the set { ^, array, integer, id, char }
Recursive-descent without backtracking: if the grammar contains two rules...
...then FIRST(something) and FIRST(somethingelse) must be disjoint (=no common elements).NT -> something NT -> somethingelse
Use opt_stmts -> empty if nothing else matches opt_stmts, which will be when lookahead is end.stmt -> begin opt_stmts end opt_stmts -> stmt_list | empty
Implementation of a predictive, recursive-descent parser:expr -> expr + term
void expr() {
if (lookahead == num or lookahead == id)
expr();
else
...
Eliminate left recursion!
Rewrite this left-recursive production:
into these, which are not left-recursive:A -> A x | y
Example: rewrite this left-recursive production:A -> y R R -> x R | empty
into these, which are not left-recursive:expr -> expr + term | term
x = + termexpr -> term rest rest -> + term rest | empty
ASU Fig 2.13/2.19 translations scheme for the program in 2.5:
expr -> expr + term { print('+') }
expr -> expr - term { print('-') }
expr -> term
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
Remember that term -> term + term was ambiguous
(Sw: tvetydig), so we transformed the grammar.
Rewrite the grammar to eliminate left recursion.
Important: Handle the semantic actions as part of the grammar,
when you rewrite it using the left-recursion elimination technique from above,
to get the prints done at the right places!
expr -> term rest
rest -> + term { print('+') } rest
rest -> - term { print('-') } rest
rest -> empty
term -> 0 { print('0') }
term -> 1 { print('1') }
term -> 2 { print('2') }
...
term -> 9 { print('9') }
The interesting parts of the program:
void term () {
if (isdigit(lookahead)) {
putchar(lookahead);
match(lookahead);
}
else
error();
}
void rest() {
if (lookahead == '+') {
match('+'); term(); putchar('+'); rest();
}
else if (lookahead == '-') {
match('-'); term(); putchar('-'); rest();
}
else
;
}
void expr() {
term(); rest();
}
Full source code: 2.5
Source code: lexer.c
Source code: symbol.c