• Skriv svaren på svenska eller engelska.
• Skriv tydligt och klart. Lösningar som inte går att läsa kan naturligtvis inte ge några poäng. Oklara och tvetydiga formuleringar kommer att misstolkas.
• Skriv den personliga tentamenskoden på varje inlämnat blad. Skriv inte namn eller personnummer på bladen.
• Skriv bara på en sida av papperet. Använd inte röd skrift.
• Antaganden utöver de som står i uppgifterna måste anges. Gjorda antaganden får inte förändra den givna uppgiften.
• Skriv gärna förklaringar om hur du tänkt. Även ett svar som är fel kan ge poäng, om det finns med en förklaring som visar att huvudtankarna var rätt.

Formelsamling

1. Eliminering av vänsterrekursion

A -> A x | y

Regeln ersätts av följande två regler (eller, korrektare uttryckt, tre produktioner), som beskriver samma språk men som inte är vänsterrekursiva:

A -> y R
R -> x R | empty

2. Vänsterfaktorisering

A -> x y | x z

Skriv om till dessa tre produktioner:

A -> x R
R -> y | z

Scenario till uppgift 1-4

(Bilden är från användaren Karophyr på engelska Wikipedia, licensierad under Creative Commons Attribution-Share Alike 2.5 Generic, 2.0 Generic och 1.0 Generic.)

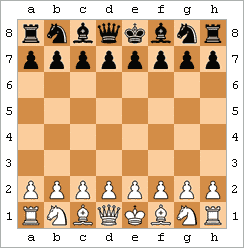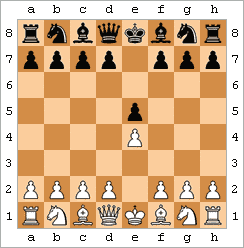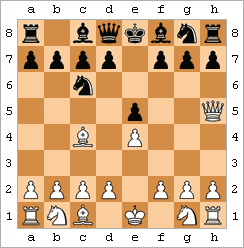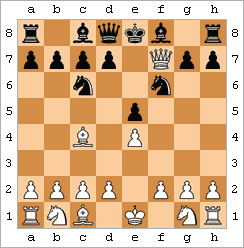
Schacknotation är ett system för att nedteckna schackpartier för senare genomgång och analys. Den vanligaste metoden är den algebraiska notationen, som bygger på schackbrädets koordinatsystem. Ett exempel med ett mycket kort parti:

1. e4 e5
2. Lc4 Sc6
3. Dh5 Sf6
4. Df7#

På varje rad anges först dragets ordningsnummer, därefter den vita spelarens drag, och sist den svarta spelarens drag. Ett drag anges med vilken sorts pjäs som flyttades och koordinaterna för den ruta som pjäsen flyttades till. Pjäsen anges med K för kung, D för dam, T för torn, L för löpare, S för springare, och ingenting för bonde. Koordinaterna består av en bokstav från a till h och en siffra från 1 till 8.

Om en av spelarna vinner och partiet tar slut anges det med tecknet #, som i exemplet ovan. Det kan komma efter den vita spelarens drag, som i exemplet, och då gör den svarta spelaren inget drag, och det kan också komma efter den svarta spelarens drag.

På riktigt är notationen krångligare, och det finns fler sorters drag, men här nöjer vi oss med beskrivningen ovan.

Uppgift 1 (4 p)

b) En del av terminalerna har inte fixa lexem, utan kan se olika ut. Skriv, för varje sådan terminal, ett reguljärt uttryck som beskriver hur den får se ut!

Uppgift 2 (5 p)

Uppgift 3 (4 p)

1. g4 e5
2. f3 Dh4#

Uppgift 4 (8 p)

Uppgift 5 (8 p)

x = 1; y = 2; while (z < t) { x = y * z + t / u / v + w; } while (x > y) { y = r + s + t * u * v; x = w; }

Översätt ovanstående programavsnitt till två av följande tre representationer. (Skulle du svara på alla tre, räknas den med högst poäng bort.)

a) ett abstrakt syntaxträd (genom att rita upp trädet!)
b) postfixkod för en stackmaskin
c) treadresskod

Observera: Två av typerna, inte alla tre!

Uppgift 6 (6 p)

b) Referensräkning har problem med en viss sorts datastrukturer. Förklara med ett exempel.

c) Hur kan man lösa det problemet?

Uppgift 7 (5 p)

#include <stdlib.h>
#include <stdio.h>

int x, y, z;

void f(int a, int b) {
    int z;
    x = 1;
    y = 2;
    z = 3;
    int* p;
    p = malloc(sizeof(int));
    *p = a;
    if (a < 4)
        f(a + 5, b + 6);
    else
        printf("Här!\n");
}

int main(void) {
    int x, y;
    x = 7;
    y = 8;
    z = 9;
    f(0, y);
}

Funktionen main anropar funktionen f, som i sin tur kan anropa sig själv rekursivt. När programexekveringen i kommer fram till utskriften "Här!", antar vi att vi stoppar programmet och tittar på vilka olika variabler som finns i minnet.

I minnet kommer det då att finnas ett antal lagringsutrymmen för heltal, som innehåller några olika värden. Rita upp en skiss över dessa variabler, och förklara vad som är vad. Din förklaring bör bland annat innehålla termerna "statiska data", "stack", "heap", "aktiveringspost" och "parametrar".