Kompilatorer och interpretatorer: Tentamen 2023-03-13

Örebro universitet
Institutionen för naturvetenskap och teknik
Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se)

Tentamen i

Kompilatorer och interpretatorer

måndag 13 mars 2023

Gäller som tentamen för:
DT501A Kompilatorer och interpretatorer för civilingenjörer, provkod A001

Hjälpmedel:	Ordbok för översättning.
Poängkrav:	Maximal poäng är 48. För godkänt betyg krävs totalt minst 25 poäng.
Resultat:	Meddelas senast 15 arbetsdagar efter tentamensdatum.
Återlämning av tentor:	Elektroniskt via webbportalen Studenttjänster.
Examinator och jourhavande:	Thomas Padron-McCarthy, telefon 070 - 73 47 013.

Skriv svaren på svenska eller engelska.
Skriv tydligt och klart. Lösningar som inte går att läsa kan naturligtvis inte ge några poäng. Oklara och tvetydiga formuleringar kommer att misstolkas.
Skriv den personliga tentamenskoden på varje inlämnat blad. Skriv inte namn eller personnummer på bladen.
Skriv bara på en sida av papperet. Använd inte röd skrift.
Antaganden utöver de som står i uppgifterna måste anges. Gjorda antaganden får inte förändra den givna uppgiften.
Skriv gärna förklaringar om hur du tänkt. Även ett svar som är fel kan ge poäng, om det finns med en förklaring som visar att huvudtankarna var rätt.

LYCKA TILL!

Formelsamling

1. Eliminering av vänsterrekursion

En vänsterrekursiv grammatik kan skrivas om så att den inte är vänsterrekursiv. Antag att en regel (eller, korrektare uttryckt, två produktioner) i grammatiken ser ut så här:

A -> A x | y

A är en icke-terminal, men x och y står för godtyckliga konstruktioner som består av terminaler och icke-terminaler.

Regeln ersätts av följande två regler (eller, korrektare uttryckt, tre produktioner), som beskriver samma språk men som inte är vänsterrekursiva:

A -> y R
R -> x R | empty

2. Vänsterfaktorisering

Antag att grammatiken innehåller denna regel (två produktioner):

A -> x y | x z

A är en icke-terminal, men x, y och z står för godtyckliga konstruktioner som består av terminaler och icke-terminaler.

Skriv om till dessa tre produktioner:

A -> x R
R -> y | z

Uppgift 1 (10 p)

Beskriv kort vad var och en av följande tio saker är, och ange vilken av kompilatorns faser den hör ihop med!

a) basic block
b) copy propagation
c) eliminering av svansrekursion
d) eliminering av vänsterrekursion
e) lexem
f) operatorassociativitet
g) reduce-reduce-konflikt
h) registerallokering
i) startsymbol
j) Yacc

Uppgift 2 (7 p)

Det här är ett programavsnitt i ett C-liknande språk:

if (a == b) {
    c = d + e + f * g;
    if (h == i) {
        k = m;
        n = p;
    }
    q = r;
}
else {
    s = t * u * z;
}

Översätt ovanstående programavsnitt till två av följande tre typer av mellankod. (Skulle du svara på alla tre, räknas den med högst poäng bort.)

a) ett abstrakt syntaxträd (genom att rita upp trädet!)
b) postfixkod för en stackmaskin
c) treadresskod

Observera: Två av typerna, inte alla tre!

Uppgift 3 (7 p)

Här är en grammatik. Kursiverade namn är icke-terminaler. Namn i fetstil är terminaler. Startsymbolen är S.

S -> a b T
T -> c d | c T

a) Grammatiken är inte lämplig för att implementeras med en prediktiv recursive-descent-parser med en token lookahead (en LL(1)-parser). Förklara varför! Vad skulle hända om vi försökte?

b) Visa hur inmatningen a b c c c d parsas av en bottom-up-parser med en stack. Visa vilka skift- och reduce-operationer som utförs, och hur stacken ser ut efter varje operation.

c) Skriv om grammatiken så den kan implementeras med en top-down-parser av LL(1)-typ. Visa också vilka grammatiktransformationer som användes.

Scenario till övriga uppgifter

En graf består av noder ("vertices" på engelska) och bågar ("edges" på engelska). Här är en graf med fem noder som är hopkopplade med sex bågar:

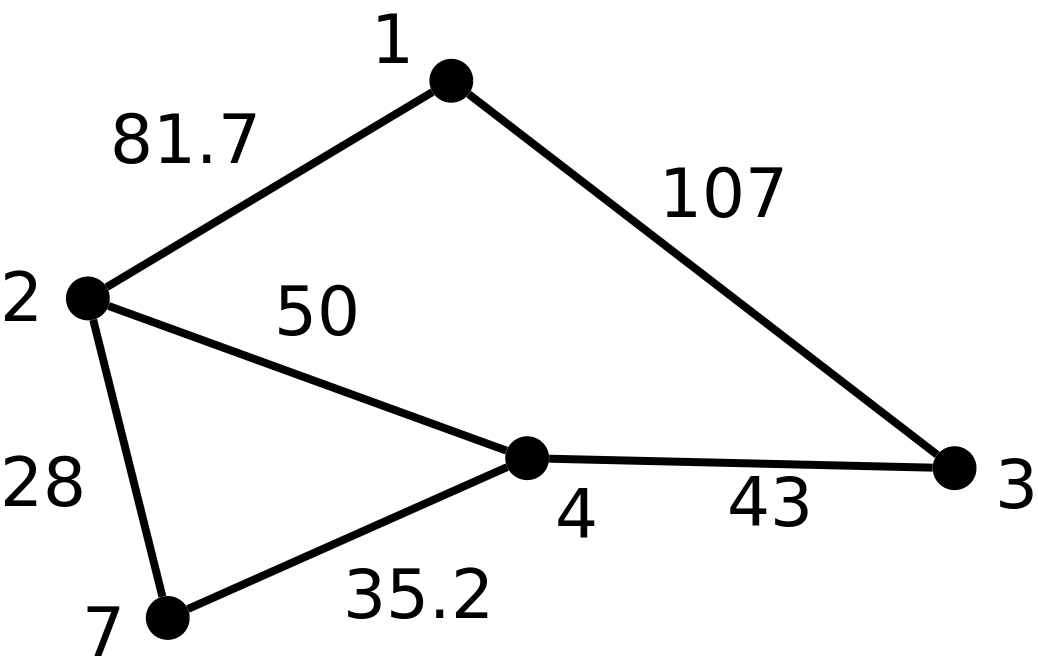
Bågarna har vikter. Till exempel har bågen som kopplar ihop nod nummer 4 och nod nummer 7 vikten 35.2.

Nu vill vi skapa ett språk för att beskriva grafer. Grafen på bilden ovan kan beskrivas så här:

{
    vertex 1;
    vertex 2;
    edge 1 2 81.7;
    vertex 3;
    edge 1 3 107;
    vertex 7;
    edge 2 7 28;
    vertex 4;
    vertex 5;
    edge 2 4 50;
    edge 7 4 35.2;
    edge 4 3 43;
}

Som vi kan se ska hela inmatningen skrivas inom måsvinge-klamrar, och det finns två kommandon, vertex för att ange en nod och edge för att ange en båge. Alla kommandona avslutas med semikolon. Noderna anges med positiva heltal, och vikterna är positiva tal som kan ha decimaler. Bågarna antas vara dubbelriktade, så det spelar ingen roll i vilken ordning man anger de två noderna i ett edge-kommando.

Inmatningen kan skrivas på fritt format. Exempelvis är nedanstående inmatning syntaktiskt ekvivalent med den i exemplet ovan.

          {vertex 1;vertex 2;edge 1 2 81.7;vertex 3;
edge 1 3 107;vertex 7;edge 2 7

28
;    vertex 4;vertex 5;edge 2 4 50;edge 7 4 35.2;edge 4 3 43;}

Uppgift 4 (4 p)

a) Vilka terminaler behövs för att man ska kunna skriva en grammatik för språket i scenariot?

b) En del av terminalerna har inte fixa lexem, utan kan se olika ut. Skriv, för varje sådan terminal, ett reguljärt uttryck som beskriver hur den får se ut!

Uppgift 5 (5 p)

Skriv en grammatik för språket. Startsymbolen ska vara inmatning, som representerar en komplett inmatning enligt scenariot ovan.

Uppgift 6 (5 p)

Ett parse-träd (ibland kallat "konkret syntaxträd") innehåller noder för alla icke-terminaler. Rita upp parse-trädet för den här inmatningen, enligt din grammatik i uppgiften ovan:

{ vertex 100; edge 1 2 3; vertex 200; }

Uppgift 7 (2 p)

I grafen ovan anges noder med nummer 100 och 200, men en båge mellan noder med nummer 1 och 2. Det är förstås fel på något sätt. Men hur påverkar det felet:

a) scannern?
b) parsern?

Uppgift 8 (8 p)

Skriv en prediktiv recursive-descent-parser för språket i ett språk som åtminstone liknar C, C++, C# eller Java. Du behöver inte skriva exakt korrekt programkod, men det ska framgå vilka procedurer som finns, hur de anropar varandra, och vilka jämförelser med tokentyper som görs. Du kan anta att det finns en funktion som heter scan, som returnerar typen på nästa token, och en funktion som heter error, som man kan anropa när något gått fel och som skriver ut ett felmeddelande och avslutar programmet.