Databasteknik: Lösningar till tentamen 2021-05-31

Observera att detta är förslag på lösningar. Det kan finnas andra lösningar som också är korrekta. Det kan hända att en del av lösningarna är mer omfattande än vad som krävs för full poäng på uppgiften, eller att de bara hänvisar till var man kan läsa svaren. Dessutom har det inträffat i världshistorien att lärare skrivit fel i lösningsförslagen. Jag har förstås aldrig gjort det, men andra. Är det verkligen någon som läser såna här inledande texter? Jag vet inte. Det kan vara så. Rabarber rabarber rabarber. Det har jag hört att statisterna får säga på filminspelningar när det ska vara bakgrundssorl från en restaurang eller liknande. Här nedan kommer lösningsförslagen till uppgifterna.

Uppgift 1 (6 p)

Rita ett ER- eller EER-diagram för den beskrivna databasen. Använd informationen i scenariot ovan, men tänk också på att det ska gå att svara på frågorna i uppgift 3 nedan.

ER- och EER-diagram kan ritas på flera olika sätt. Om du använder en annan notation än kursboken, måste du förklara den notation som du använder.

ER-diagram

Uppgift 2 (8 p)

Implementera den beskrivna databasen i relationsmodellen, dvs översätt ER-diagrammet till tabeller. Implementationen ska vara bra.

a) Visa en tydlig översikt över dina tabeller. Ange vilka relationer som finns och vilka attribut varje relation innehåller, med väl valda exempeldata. Ange också alla kandidatnycklar, vilken av dessa som är primärnyckel, samt vilka referensattribut som finns och vad de refererar till.

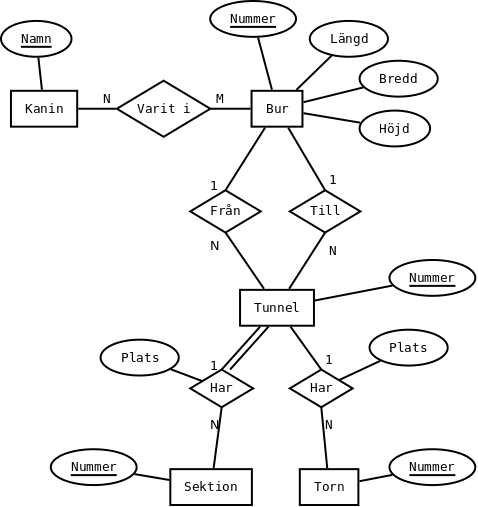
Burar(Nummer, Längd, Bredd, Höjd)
Tunnlar(Nummer, Från, Till)
Rörsektioner(Nummer, Tunnel, Plats)
Utsiktstorn(Nummer, Tunnel, Plats)
Kaniner(Nummer, Namn)
Besökt(Kanin, Bur)

Kandidatnycklar är understrukna. I de tabeller där det finns flera kandidatnycklar är den första primärnyckel.

Referensattribut:

Tunnlar.Från till Burar.Nummer
Tunnlar.Till till Burar.Nummer
Rörsektioner.Tunnel till Tunnlar.Nummer
Utsiktstorn.Tunnel till Tunnlar.Nummer
Besökt.Kanin till Kaniner.Nummer
Besökt.Bur till Burar.Nummer

Tabellerna med exempeldata:

Burar
Nummer Längd Bredd Höjd
1 120 100 50
2 130 100 50
3 130 100 50

Tunnlar
Nummer Från Till
1 1 2
2 2 3
17 3 1

Rörsektioner
Nummer Tunnel Plats
1 1 1
2 1 2
3 17 1

Utsiktstorn
Nummer Tunnel Plats
1 2 1
2 2 2
3 17 2

Kaniner
Nummer Namn
1 Godis
2 Snöpricken
3 Lakrits
4 Fläcken
5 Stampe

Besökt
Kanin Bur
1 1
2 1
2 2
3 1
3 2
4 1

b) Skriv de SQL-kommandon som behövs för att skapa tabellerna, med lämpliga integritetsvillkor. 

CREATE TABLE Burar
(Nummer INTEGER NOT NULL PRIMARY KEY,
Längd INTEGER NOT NULL,
Bredd INTEGER NOT NULL,
Höjd INTEGER NOT NULL);

CREATE TABLE Tunnlar
(Nummer INTEGER NOT NULL PRIMARY KEY,
Från INTEGER NOT NULL REFERENCES Burar(Nummer),
Till INTEGER NOT NULL REFERENCES Burar(Nummer));

CREATE TABLE Rörsektioner
(Nummer INTEGER NOT NULL PRIMARY KEY,
Tunnel INTEGER NOT NULL REFERENCES Tunnlar(Nummer),
Plats INTEGER NOT NULL CHECK (Plats >= 1),
UNIQUE (Tunnel, Plats));

CREATE TABLE Utsiktstorn
(Nummer INTEGER NOT NULL PRIMARY KEY,
Tunnel INTEGER NOT NULL REFERENCES Tunnlar(Nummer),
Plats INTEGER NOT NULL CHECK (Plats >= 1),
UNIQUE (Tunnel, Plats));

CREATE TABLE Kaniner
(Nummer INTEGER NOT NULL PRIMARY KEY,
Namn VARCHAR(15) NOT NULL UNIQUE);

CREATE TABLE Besökt
(Kanin INTEGER NOT NULL REFERENCES Kaniner(Nummer),
Bur INTEGER NOT NULL REFERENCES Burar(Nummer),
PRIMARY KEY (Kanin, Bur));
För att underlätta provkörningar visas här också INSERT-kommandon med exempeldata: 
INSERT INTO Burar (Nummer, Längd, Bredd, Höjd) VALUES (1, 120, 100, 50);
INSERT INTO Burar (Nummer, Längd, Bredd, Höjd) VALUES (2, 130, 100, 50);
INSERT INTO Burar (Nummer, Längd, Bredd, Höjd) VALUES (3, 130, 100, 50);

INSERT INTO Tunnlar (Nummer, Från, Till) VALUES (1, 1, 2);
INSERT INTO Tunnlar (Nummer, Från, Till) VALUES (2, 2, 3);
INSERT INTO Tunnlar (Nummer, Från, Till) VALUES (17, 3, 1);

INSERT INTO Rörsektioner (Nummer, Tunnel, Plats) VALUES (1, 1, 1);
INSERT INTO Rörsektioner (Nummer, Tunnel, Plats) VALUES (2, 1, 2);
INSERT INTO Rörsektioner (Nummer, Tunnel, Plats) VALUES (3, 17, 1);

INSERT INTO Utsiktstorn (Nummer, Tunnel, Plats) VALUES (1, 2, 1);
INSERT INTO Utsiktstorn (Nummer, Tunnel, Plats) VALUES (2, 2, 2);
INSERT INTO Utsiktstorn (Nummer, Tunnel, Plats) VALUES (3, 17, 2);

INSERT INTO Kaniner (Nummer, Namn) VALUES (1, 'Godis');
INSERT INTO Kaniner (Nummer, Namn) VALUES (2, 'Snöpricken');
INSERT INTO Kaniner (Nummer, Namn) VALUES (3, 'Lakrits');
INSERT INTO Kaniner (Nummer, Namn) VALUES (4, 'Fläcken');
INSERT INTO Kaniner (Nummer, Namn) VALUES (5, 'Stampe');

INSERT INTO Besökt (Kanin, Bur) VALUES (1, 1);
INSERT INTO Besökt (Kanin, Bur) VALUES (2, 1);
INSERT INTO Besökt (Kanin, Bur) VALUES (3, 1);
INSERT INTO Besökt (Kanin, Bur) VALUES (4, 1);
INSERT INTO Besökt (Kanin, Bur) VALUES (2, 2);
INSERT INTO Besökt (Kanin, Bur) VALUES (3, 2);

SELECT * FROM Burar;
SELECT * FROM Tunnlar;
SELECT * FROM Rörsektioner;
SELECT * FROM Utsiktstorn;
SELECT * FROM Kaniner;
SELECT * FROM Besökt;

Uppgift 3 (12 p)

Formulera följande frågor i SQL. Definiera gärna vyer eller CTE:er om det underlättar, men skapa inte nya tabeller.

a) (1p) Hur höga är de burar som är längre än 120 centimeter? Vi vill veta varje sådan burs nummer och höjd. 

SELECT Nummer, Höjd
FROM Burar
WHERE Längd > 120;

b) (1p) Vi ställer alla burarna ovanpå varandra. Hur hög blir stapeln? 

SELECT SUM(Höjd) FROM Burar;

c) (2p) Hur stor golvyta (dvs längden multiplicerad med bredden) har buren som har lägst nummer? 

SELECT Längd * Bredd
FROM Burar
WHERE Nummer IN (SELECT MIN(Nummer) FROM Burar);

d) (2p) Hur många kaniner har besökt varje bur? Vi vill ha ett svar som består av två kolumner: burens nummer och antalet kaniner som besökt buren. Det är inte att krav att burar som ingen kanin ännu har besökt ska vara med i svaret. 

SELECT Burar.Nummer, COUNT(*) AS Antal
FROM Burar, Besökt
WHERE Burar.Nummer = Besökt.Bur
GROUP BY Burar.Nummer;
En alternativ lösning: 
SELECT Burar.Nummer, COUNT(*) AS Antal
FROM Burar JOIN Besökt ON Burar.Nummer = Besökt.Bur
GROUP BY Burar.Nummer;
Eller bara: 
SELECT Bur, COUNT(*) AS Antal
FROM Besökt
GROUP BY Bur;

e) (1p) Om svaret ska ha med de burar som ingen kanin ännu har besökt, med antalet noll, behöver man skriva frågan på ett visst sätt. Hur?

Man måste använda en yttre join. Man kan inte heller skriva "COUNT(*)". 

SELECT Burar.Nummer, COUNT(Besökt.Kanin) AS Antal
FROM Burar LEFT JOIN Besökt ON Burar.Nummer = Besökt.Bur
GROUP BY Burar.Nummer;

f) (2p) Förklara varför man måste göra så.

Med en vanlig join, även kallad inre join, tar man inte med de rader som inte går att para ihop med en rad från den andra tabellen, Därför försvinner de burar som ingen kanin besökt redan vid sammanslagningen ("joinen") av tabellerna Burar och Besökt,

Om man använder "COUNT(*)" räknar man rader, inklusive rader med NULL, så obesökta burar får antalet 1.

g) (3p) Vad heter de kaniner som varit i någon av de burar som kaninen Lakrits varit i? 

SELECT Namn
FROM Kaniner
WHERE Nummer IN (SELECT Kanin
                 FROM Besökt
                 WHERE Bur IN (SELECT Bur
                               FROM Besökt
                               WHERE Kanin IN (SELECT Nummer
                                               FROM Kaniner
                                               WHERE Namn = 'Lakrits')));
En alternativ lösning: 
SELECT Andra.Namn
FROM Kaniner AS Lakrits, Kaniner AS Andra, Bur, Besökt AS Lakritsbesök, Besökt AS Andrabesök
WHERE Andra.Nummer = Andrabesök.Kanin
AND Andrabesök.Bur = Lakritsbesök.Bur
AND Lakritsbesök.Kanin = Lakrits.Nummer
AND Lakrits.Namn = 'Lakrits';

Uppgift 4 (3 p)

Du skapar databasen enligt uppgifterna ovan, med de CREATE TABLE-kommandon du skrev i uppgift 2, och så lägger vi in de kaniner, burar och tunnlar som vi har i trädgården. Nu kommer någon och frågar om du inte ska skapa index också. Diskutera hur man bör göra!

Om man ska ha kaninerna hemma i trädgåden har man förmodligen bara några få burar och tunnlar. Det är svårt att tänka sig en trädgård med mer än hundra burar och låt oss säga tusen rörsektioner. Det är också svårt att tänka sig att databasen kommer utsättas för stor belastning med många samtidiga användare och många frågor. Därför kommer prestanda förmodligen att vara tillräckliga redan utan index, och man behöver inte skapa några index alls.

Skulle databasen växa och bli mycket större, till exempel för att någon excentrisk miljardär skaffar sig miljoner kaniner och burar i parken på sitt slott, och kanske också gör en webbplats så att människor i hela världen kan söka i databasen, kan man behöva bättre prestanda, och då måste man skapa index.

Då är frågan vilka index man ska skapa. Det beror på vilka sökningar man gör i databasen, för orsaken till att man skapar index är att göra sökningar snabbare. Om vi antar att det är sökningarna i uppgift 3 som ska gå snabbare, behöver vi titta på vilka kolumner som används för att hitta rader i tabeller, dvs (ungefär) nämns i WHERE-villkoren, inklusive JOIN-villkor.

De flesta vanliga databashanterarna brukar automatiskt skapa index på allt som man deklarerat som PRIMARY KEY och UNIQUE, dels för att man kan räkna med att man ofta använder dem i sökningar, och dels för att underlätta för databashanteraren att kontrollera att det inte blir dubbletter. Därför kan vi räkna med att man inte behöver skapa nya index på dessa. Tänk dock på att i sammansatta index, som indexet på primärnyckeln i tabellen Besökt, har man bara nytta av indexet när man söker på ett prefix av de ingående kolumnerna.

Med databasen och frågorna från lösningsförslagen ovan bör man skapa dessa index:

Om den här databasen saknar de automatiskt skapade unika indexen:

Uppgift 5 (3 p)

Ett index är en datastruktur som databashanteraren använder för att snabbt hitta data i en tabell. Tre olika typer av datastrukturer som man kan använda är binära träd, B-träd och hashtabeller.

Vilken av de tre datastrukturerna är vanligast i normala databashanterare som Mimer och MySQL, och varför har man valt just den i stället för de andra?

B-träd. Ofta används varianter som B+-träd och B*-träd.

(En kommentar om själva namnet: Det är oklart vad "B":et egentligen står för. Det står inte i den ursprungliga rapporten om B-träd. Det kan vara "balanserat", eller "balanserande", som i "självbalanserande", men en av dem som uppfann B-träd hette Bayer, och han arbetade på Boeing. Eftersom B-träd är en generalisering av binära träd skulle det också kunna vara första bokstaven i "binär".)

Eftersom B-träd kan ha fler underträd under varje nod, ofta flera hundra, blir de bredare och därför lägre än binära träd, och man behöver inte besöka lika många noder när man söker i trädet. Å andra sidan tar det längre tid inuti varje nod, eftersom man ska hitta vilket av alla underträden man ska gå ner i, men det är en bra avvägning om det är dyrt (dvs tar lång tid) att besöka en nod, men billigt att sen arbeta inuti den noden. Det gäller om noderna är lagrade på sekundärminne (hårddisk eller SSD), alternativt i primärminne med ett mycket snabbare cacheminne. Databaser är ofta större än vad som får plats i primärminnet, så man brukar räkna med att de finns (huvudsakligen) på sekundärminne. Tidskomplexiteten för sökning i B-träd är, precis som för binära träd, logaritmisk, men tiderna för (välbalanserade) binära träd är 2-logaritmen av datamängden, medan tiderna för ett B-träd av ordningen 100 är 100-logaritmen. Det gör att söktiderna ökar mycket långsamt när datamängden ökar. Om man räknar antalet läsningar från sekundärminne ökar tiden med en sådan läsning per faktor 100, så om en enkel sökning i en miljon poster tar 3 diskläsningar tar samma sökning i 100 miljoner poster 4 diskläsningar. På en mekanisk hårddisk kan man räkna med att tiden ökar med 0.01 sekunder, och på en SSD med 0.0001 sekunder.

Det finns varianter av binära träd som balanseras automatiskt, och i en riktig tillämpning skulle man knappast använda obalanserade binära träd. Orsaken till att man använder B-träd i stället för binära träd är därför inte att B-träd är balanserade, utan orsaken är att B-träden är lägre, så man behöver besöka färre noder.

Hashtabeller kan vara snabbare än B-träd för att hitta ett bestämt värde, men dels fungerar de inte för att hitta delar av en sökterm (till exempel i ett villkor som WHERE Name LIKE 'Sven%'), och det går inte att via hashtabellen ta fram poster i sorterad ordning. B-träd klarar båda dessa saker. (Däremot klarar inte heller B-träd en sökning som WHERE Name LIKE '%sson'.)

Det finns varianter av hashtabeller som växer automatiskt och inkrementellt när det behövs, så det är inte ett problem att man måste dimensionera dem i förväg, eller att de innehåller mycket tomrum.

Uppgift 6 (3 p)

Vi använder en databashanterare med auto-commit, vilket betyder att varje SQL-kommando räknas som en egen transaktion, så länge man inte uttryckligen startar en transaktion med kommandot "start transaction".

Vi startar två olika klientprogram som loggar in på samma databas, och ger följande SQL-kommandon, i den angivna ordningen, i de två klienterna.

Vad blir resultatet av var och en av de nio select-frågorna? (På nästa sida!)

Klient 1 Klient 2
create table Kaniner
(nummer integer not null primary key,
färg varchar(10)); 		 
insert into Kaniner values (1, 'vit');  
  insert into Kaniner values (2, 'svart');
select * from Kaniner; -- Fråga 1  
  select * from Kaniner; -- Fråga 2
start transaction;  
insert into Kaniner values (3, 'svart');  
select * from Kaniner; -- Fråga 3  
  select * from Kaniner; -- Fråga 4
rollback;  
  select * from Kaniner; -- Fråga 5
start transaction;  
insert into Kaniner values (3, 'vit');  
select * from Kaniner; -- Fråga 6  
  select * from Kaniner; -- Fråga 7
commit;  
select * from Kaniner; -- Fråga 8  
  select * from Kaniner; -- Fråga 9
Fråga 1:

nummer färg
1 vit
2 svart

Fråga 2:

nummer färg
1 vit
2 svart

Fråga 3:

nummer färg
1 vit
2 svart
3 svart

Fråga 4 (eventuellt efter en paus medan den väntar på låset):

nummer färg
1 vit
2 svart

Fråga 5:

nummer färg
1 vit
2 svart

Fråga 6:

nummer färg
1 vit
2 svart
3 vit

Fråga 7 (men det beror på transaktionsmekanismerna i databashanteraren)

nummer färg
1 vit
2 svart

Fråga 8:

nummer färg
1 vit
2 svart
3 vit

Fråga 9:

nummer färg
1 vit
2 svart
3 vit

Uppgift 7 (5 p)

Tabellen Kaniner i uppgiften ovan är ganska enkel. Vi lägger till kolumner för längd och vikt, med vikten uttryckt både i kilo och gram:

Nummer Färg Längd Kilo Gram
1 Vit 39 2.1 2100
3 Vit 45 2.3 2300
2 Vit 35 1.8 1800
17 Vit 35 1.9 1900

a) Skriv ALTER TABLE-kommandon för att lägga till de två tre nya kolumnerna. 

ALTER TABLE Kaniner ADD Längd INTEGER;
ALTER TABLE Kaniner ADD Kilo DECIMAL(2,1);
ALTER TABLE Kaniner ADD Gram INTEGER;
b) Vad är primärnyckel i den här nya tabellen?
Nummer, precis som förut
c) Vilka kandidatnycklar, förutom primärnyckeln, finns i tabellen?
Inga.
d) Vilka fullständiga funktionella beroenden finns i tabellen?
Nummer till Färg
Nummer till Längd
Nummer till Kilo
Nummer till Gram
Kilo till Gram
Gram till Kilo
e) Vilka av de normalformer som ingår i kursen (1NF, 2NF, 3NF och BCNF) uppfyller tabellen? Motivera svaret!
1NF eftersom varje ruta i tabellen bara innehåller enkla, atomära värden. 2NF eftersom den inte har någon sammansatt kandidatnyckel, och därför kan det inte finnas några beroende på delar av en kandidatnyckel. Inte 3NF eller högre normalformer (dvs BCNF) eftersom det finns ffb mellan ickenyckelattribut (Kilo och Gram).

Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se), 15 juni 2021