
Om en integer lagras i databasen med 32 bitar, dvs 4 byte, och en float med 64 bitar, dvs 8 byte, är poststorleken för tabellen Buskar 4 + 8 + 8 + 8 dvs 28 byte, och för tabellen Blåbär 4 + 8 + 8 + 4 dvs 24 byte. En grov uppskattning är att databasen, med diverse tomrum och index, tar upp dubbelt så mycket plats som det rena datat, dvs 2 * (107 * 28 + 109 * 24) byte = 50 gigabyte.
För en bättre uppskattning räknar vi med B+-trädsindex, Den genomsnittliga fyllnadsgraden i såväl indexblock som indexstyrda lövblock är 2/3. Vi antar en blockstorlek på 2 kilobyte (2048 byte). Blockpekare är 64 bitar, dvs 8 byte.
Tabellen Buskar och dess index:
Blockningsfaktorn för datablock i Buskar är 2048 / 28 = 73, och fyllnadsgraden 2/3 ger en effektiv blockningsfaktor på 48.7. Antalet datablock blir 107 / 48.7 = 205339. Datafilen innehåller alltså 205339 diskblock. (Datablocken kan ha en vidarepekare till nästa block i datafilen, för att enkelt kunna traversera blocken sekvensiellt om inte alla blocken ligger i ordning på disken, men det ignorerar vi här.)
Primärindexet för Buskar har blockningsfaktorn (2048 - 8) / (4 + 8) + 1 = 171, och den effektiva blockningsfaktorn 114.0. (På den lägsta indexnivån, alltså lövnoderna i indexet som innehåller pekare till datablocken, kan man ha en vidarepekare till nästa indexblock på den nivån, för att enkelt kunna traversera indexet sekvensiellt, men det ignorerar vi här.) Det ger 205339 / 114 = 1802 (avrundat uppåt) indexblock på lägsta nivån, 16 indexblock på nästa nivå, och ett rotblock. Indexträdets djup är 3, och upptar 1819 diskblock.
Buskar har också två sekundärindex, på latitud och longitud. Bägge är på datatypen float, och har blockningsfaktorn (2048 - 8) / (8 + 8) + 1 = 128, och den effektiva blockningsfaktorn 85.3. Eftersom de är sekundärindex antar vi att de är täta index, dvs med en indexpost för varje datapost, vilket ger 107 / 85.3 = 117234 indexblock på lägsta nivån, 1375 indexblock på nästa nivå, 17 på nästa, och ett rotblock. Indexträdets djup är 4, och upptar 118627 diskblock.
Tabellen Blåbär och dess index:
Blockningsfaktorn för datablock i Blåbär är 2048 / 24 = 85, och fyllnadsgraden 2/3 ger en effektiv blockningsfaktor på 56.7. Antalet datablock blir 109 / 56.7 = 17636684. Datafilen innehåller alltså cirka 18 miljoner diskblock.
Primärindexet för Blåbär har precis som för Buskar blockningsfaktorn (2048 - 8) / (4 + 8) + 1 = 171, och den effektiva blockningsfaktorn 114.0. Det ger 154708 indexblock på lägsta nivån, 1358 indexblock på nästa nivå, 12 indexblock på nästa nivå, och ett rotblock. Indexträdets djup är 4, och upptar 156079 diskblock.
Blåbär har också ett sekundärindex på kolumnen buske. Det är på datatypen int, och har blockningsfaktorn (2048 - 8) / (4 + 8) + 1 = 171, och den effektiva blockningsfaktorn 114.0. Eftersom det är ett sekundärindex ger detta 109 / 114.0 = 8771930 indexblock på lägsta nivån, 76947 indexblock på nästa nivå, 675 på nästa, 6 på nästa, och ett rotblock. Indexträdets djup är 5, och upptar 8849559 diskblock.
Totalt upptar databasens data och index 205339+1819+118627+118627+17636684+156079+8849559, dvs 27086734 diskblock, eller 55 gigabyte.
Med en annan storlek på blocken får man förstås ett annat antal block, men storleken räknad i gigabyte blir ungefär samma.
Dessutom tillkommer datakatalogen, men den är långt under en enda gigabyte.
En normal, modern (2016) skrivbordsdator eller bärbar dator har en hårddisk eller SSD på 500-1000 gigabyte, eller ibland mycket mer, så databasen får utan problem plats på disken.
b)
Databashanteraren måste läsa hela datafilen, dvs alla 17636684 diskblock. En databashanterare med en bra fysisk datahanterare kommer att lägga diskblocken (ganska) sekvensiellt på disken.
Om vi räknar med 1 ms per diskblock vid sekvensiell läsning tar det cirka 5 timmar.
Sen är det kanske onödigt pessimistiskt att räkna med 1 millisekund per block när man läser sekvensiellt, även om det står så i boken. Siffran är nog lite föråldrad, och med moderna diskar och moderna gränssnitt som S-ATA går det fortare, så man ska nog hellre titta på mängden data och vad disken har för överföringshastighet. Som ett experiment provade jag att läsa igenom en stor fil på min vanliga skrivbordsdator, och det tog 34 sekunder att läsa cirka 4 gigabyte data, dvs ungefär 120 megabyte i sekunden. Det bör gå ungefär med samma hastighet att läsa från databasen, och då kommer vi ner i 5 minuter.
Dessutom tillkommer tid för frågeprocessning, som att parsa och analysera SQL-frågetexten, att slå upp saker i datakatalogen (som också innebär diskläsningar, om de delarna inte råkade vara cachade i primärminne), optimerarens arbete, hantering av lås och loggfil. Men allt detta tar på sin höjd någon sekund, och är försumbart i förhållande till tider på minuter och timmar.
Tiderna kan också minskas, om vissa data fanns cachade i primärminne.
c)
Ett indexet på kolumnen vikt kan användas för att snabbt hitta blåbär utgående från deras vikter, och det har vi ingen nytta av här, där frågan ändå måste gå igenom alla blåbären.
Däremot kan vi i vissa fall använda indexet för att snabba upp summeringen, om vi kan köra hela frågan enbart genom att använda indexet. Om vi antar ett tätt index, dvs ett index med en indexpost för varje datapost, så kommer blockningsfaktorn att vara (2048 - 8) / (8 + 8) + 1 = 128, den effektiva blockningsfaktorn 85.3, och på lägsta nivån får vi då 11723330 diskblock. Eftersom alla blåbärens vikter finns direkt i indexet, på den lägsta nivån, kan vi ignorera datafilen med sina 17636684 diskblock, och enbart läsa de 11723330 diskblocken i indexets lägsta nivå. Det är ungefär 2/3 av antalet i datafilen. Om det verkligen blir snabbare beror på hur sekvensiellt den fysiska datahanteraren lyckats lägga ut de blocken på disken.
select "Blåbär".* from "Blåbär", Buskar where "Blåbär".buske = Buskar.nummer and Buskar.latitud > 59 and Buskar.latitud < 59.01 and Buskar.longitud > 17 and Buskar.longitud < 17.001 and "Blåbär".vikt > 3;a)
I uttrycket nedan ska PROJECT egentligen vara grekiska bokstaven lilla pi, SELECT ska egentligen vara grekiska bokstaven lilla sigma, och X ska vara ett kryss. I en del specifikationer av relationsalgebra tillåter man heller inte kvalificerade namn som n1.nummer, utan bara enkla namn som nummer.
PROJECTBlåbär.* ( SELECTBlåbär.buske = Buskar.nummer and Buskar.latitud > 59 and Buskar.latitud < 59.01 and Buskar.longitud > 17 and Buskar.longitud < 17.001 and Blåbär.vikt > 3 ( Blåbär X Buskar ) )
Detta relationsalgebrauttryck börjar med att beräkna en kartesisk produkt. Det är först den optimerade versionen som innehåller en join.
b)

c)
Vi börjar med att dela upp det långa selektionsvillkoret i delar, och sen "trycker" vi ned varje del så långt det går i trädet. Villkoret Blåbär.buske = Buskar.nummer behöver både Blåbär och Buskar, n1.foralder = n2.nummer så det måste komma efter den kartesiska produkten. Villkoret Blåbär.buske > 3 behöver bara Blåbär, så det kan göras direkt på Blåbär-tabellen. Resten av villkoren behöver bara Buskar, så det kan göras direkt på Buskar-tabellen.

Därefter gör vi om den kartesiska produkten som följs av en selektion till en join.
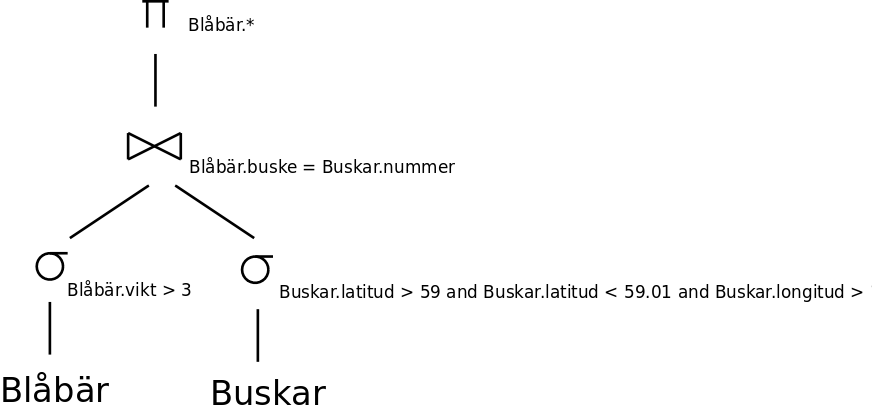
Man kan också lägga in projektioner som rensar bort onödiga kolumner.

d)
"Om det finns ett index på en kolumn i en tabell, och uttrycket innehåller en selektion på den tabellen, så börja med den selektionen."
En kostnadsbaserad frågeoptimerare har en kostnadsfunktion, som givet en exekveringsplan räknar ut den förväntade kostnaden för att köra den. Normalt betyder "kostnad" i det här sammanhanget tiden det tar att köra exekveringsplanen, och för en vanlig diskbaserad databas beror den huvudsakligen på antalet läsningar från disken. Kostnadsfunktionen kan ta hänsyn till olika algoritmer för att utföra en operation, till vilka index som finns, och till statistik om innehållet i databasen, till exempel om antal rader eller fördelningen av värden i en kolumn. Den kostnadsbaserade frågeoptimeraren jämför den förväntade kostnaden (enligt kostnadsfunktionen) för olika exekveringsplaner (antingen för alla som är möjliga, eller för ett urval av dem), och väljer den billigaste.
b)
Det finns inget index på vikt, så även om det skulle vara mycket ovanligt med blåbär som väger mer än 3 gram så kan man inte göra en snabb exekveringsplan genom att börja med att söka fram dem. Man skulle behöva läsa igenom hela blåbärstabellen.
Det finns ett index på latitud och ett på longitud, så antagligen är det bra att börja med att söka fram buskar i rätt område. Normalt kan man inte använda båda indexen, utan man måste välja ett av dem. Vilket som blir bäst beror på hur datat är fördelat, men eftersom longitud-intervallet (0.001) är mindre än latitud-intervallet (0.01) kan man spekulera att färre buskar uppfyller longitud-kravet än latitud-kravet, och att det därför skulle vara bättre att använda longitud-indexet. Vilket av de två indexen som optimeraren väljer beror på vilka data (longitud och latitud) som tabellen faktiskt innehåller, och vilken statistik om det som optimeraren har tillgång till.
Det finns ett index på kolumnen buske i tabellen Blåbär, så givet att man hittat en buske som uppfyller de geografiska kraven går det snabbt att hitta de tillhörande blåbären. Det gör det än mer troligt att det blir snabbast att börja med busktabellen, och sen slå upp i blåbärstabellen.
Vi kan jämföra med vad Mimer, som har en kostnadsbaserad optimerare, faktiskt gör. Vi fyller databasen med lite mer data än bara exempelraderna (10000 buskar och 100000 blåbär) och ger kommandot update statistics så optimeraren får tillgång till statistik om vilka data tabellerna innehåller. Vi får då följande exekveringsplan:
Start of explain result
L1:
Index lookup DBTEK0.BUSKAR using index DBTEK0.BUSKLONGITUD, end of table goto end
compare, no hit goto L1
L2:
Index scan DBTEK0.Blåbär using index DBTEK0.Växerpå, end of table goto L1
compare, no hit goto L2
Record found, goto L2
end:
End of explain result
Vi ser nu att Mimer valde att börja med indexet på longitud
för att hitta buskar i det sökta longitudintervallet,
och att den för varje sådan buske använde indexet på Blåbär.buske
för att slå upp de blåbär som växer på den busken.
Om man jämför med vad den heuristiska optimeraren kan göra, så är de tydligaste skillnaderna att den kostnadsbaserade optimeraren dels kan välja vilken sökning den ska börja med baserat på vilka index som finns, och att den sen kan välja en joinalgoritm som använder de index som finns.
Att ett tidsschema är serialiserbart betyder att det är ekvivalent med något seriellt schema, dvs ett schema där transaktionerna körs en i taget. Ekvivalens kan definieras på olika sätt, men det vanliga är konfliktekvivalens, dvs att två tidsscheman är ekvivalenta om alla par av operationer av två olika transaktioner på samma dataojekt, där minst en av operationerna är en skrivoperation, sker i samma ordning i båda schemana. Två scheman som är konfliktekvivalenta är också garanterat resultatekvivalenta, dvs om de körs kommer de att leda till samma resulterande värden i databasen.
b)
T4 arbetar med andra dataobjekt än de andra transaktionerna, så det kan inte bli några konfliktoperationer mellan den och de andra transaktionerna.
T5 körs inte samtidigt som någon av de andra transaktionerna, så det kan inte bli några konfliktoperationer mellan den och de andra transaktionerna.
c)
Nej, det är inte serialiserbart. Vi kan titta på T1 och T2 och hur de använder X. Det finns två möjliga seriella tidsscheman: antingen körs T1 först och T2 därefter, eller T2 först och T1 därefter.
Om vi antar ordningen T1-T2 ska steg 6 köras före steg 9, dvs T1 läser det gamla värdet, inte det som T2 skriver. Det stämmer med ordningen i det givna schemat. Men med ordningen T1-T2 skulle också steg 14 köras före steg 9, så databasen efteråt innehåller det värde som T2 skrev. I det givna icke-seriella schemat i uppgiften görs steg steg 14 efter steg 9. Alltså är det givna icke-seriella schemat inte konfliktekvivalent med det seriella schemat T1-T2.
Om vi i stället antar ordningen T2-T1 ska steg 14 köras före steg 9, så databasen efteråt innehåller det värde som T1 skrev. Det stämmer med ordningen i det givna schemat. Men med ordningen T2-T1 skulle också steg 9 köras före steg 6, så att T1 läser det nya värdet som T2 har skrivit. I det givna icke-seriella schemat i uppgiften görs steg steg 9 efter steg 6. Alltså är det givna icke-seriella schemat inte konfliktekvivalent med det seriella schemat T2-T1. Det är alltså inte ekvivalent med något seriellt schema, och inte serialiserbart.
d)
(Icke-strikt) tvåfaslåsning med enkla binära lås. Exakt hur tidsschemat ser ut beror på hur databashanteraren schemalägger transaktioner, till exempel vilken av två transaktioner som väntar på att låsa samma dataobjekt som får köra först. Här antar jag att vi har en enkel kö, så den som började vänta först också får låset först.
| Tid | T1 | T2 | T3 |
|---|---|---|---|
| 1 | Start | ||
| 2 | Start | ||
| 3 | Start | ||
| 4 | Lås(X) | ||
| 5 | Läs(X) | ||
| 6 | Lås(Y) | ||
| 7 | Läs(Y) | ||
| 8 | Lås(X)... | ||
| 9 | Lås(X)... | ||
| 10 | Skriv(X) | ||
| 11 | Släpp(X) | ||
| 12 | Låst(X)! | ||
| 13 | Läs(X) | ||
| 14 | Skriv(X) | ||
| 15 | Släpp(X) | ||
| 16 | Låst(X)! | ||
| 17 | Läs(X) | ||
| 18 | Lås(Y).... | ||
| 19 | Släpp(Y) | ||
| 20 | Låst(Y)! | ||
| 21 | Skriv(Y) | ||
| 22 | Släpp(X) | ||
| 23 | Släpp(Y) | ||
| 24 | Commit | ||
| 25 | Commit | ||
| 26 | Commit |