I uttrycket nedan ska PROJECT egentligen vara grekiska bokstaven lilla pi, SELECT ska egentligen vara grekiska bokstaven lilla sigma, RENAME ska egentligen vara grekiska bokstaven lilla rho, och X ska vara ett kryss. I en del specifikationer av relationsalgebra tillåter man heller inte kvalificerade namn som n1.nummer, utan bara enkla namn som nummer.
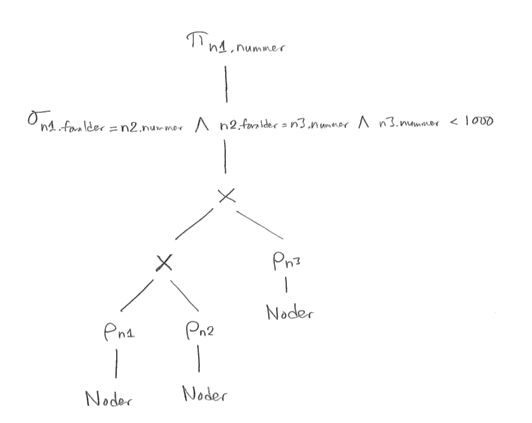
PROJECTn1.nummer ( SELECTn1.foralder = n2.nummer and n2.foralder = n3.nummer and n3.nummer < 1000 ( RENAMEn1(Noder) X RENAMEn2(Noder) X RENAMEn3(Noder) ) )
Observera att detta relationsalgebrauttryck börjar med att beräkna två kartesiska produkter. Det är först den optimerade versionen som innehåller joinar.
b)

c)
Med materialiserade mellanresultat räknas varje mellanresultat ut och lagras i sin helhet, på disk eller i primärminne, innan det kan användas i efterföljande operationer. Operationerna utförs en i taget, utan någon parallellitet.
Med strömmande mellanresultat skickas tupler från en operation vidare till nästa operation så fort de producerats, så att flera operationer kan utföras parallellt. (Det behöver inte nödvändigtvis förekomma någon parallellitet, vare sig äkta med flera processorer eller falsk med trådar som körs omväxlande, utan det kan fungera så att operationerna körs växelvis, till exempel genom att en operation efterfrågar tupler från en föregående operation, och då överlåter kontrollen till den så att den kan producera en eller flera tupler.)
d)
Vi börjar med att dela upp det långa selektionsvillkoret i tre delar, och sen "trycker" vi ned varje del så långt det går i trädet. Villkoret n1.foralder = n2.nummer behöver både n1 och n2, så det måste komma efter den kartesiska produkten n1 X n2. Villkoret n2.foralder = n3.nummer behöver n2 och n3, så det kommer efter den andra kartesiska produkten. Villkoret n3.nummer < 1000 behöver bara n3, så det kan tryckas ner ända till efter RENAMEn3.
Därefter gör vi om en kartesisk produkt följd av en (lämplig) selektion till en join.
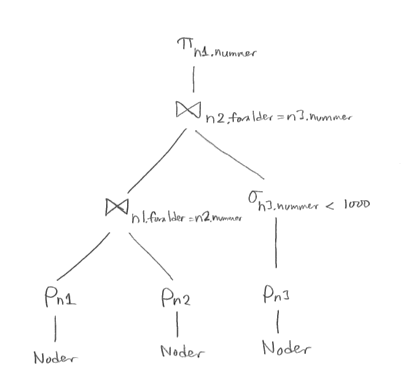
En bra heuristisk frågeoptimerare kommer antagligen också att ändra join-ordningen så att selektioner på en ensam tabell kan köras allra först. Som det är nu beräknas (om vi antar att trädet "körs" från vänster till höger) först den stora joinen mellan n1 och n2, som innehåller ungefär en miljon rader, men sen kommer bara en del av dessa rader att paras ihop med resultatet av "n3-grenen". Det vore bättre att flytta n3-grenen längst till vänster i trädet.
Ett mer detaljerat svar på en liknande uppgift finns i lösningsförslagen till tentan 2009-04-04.
e)
En (normal) heuristisk optimerare har ganska enkla regler av typen "tryck ner selektion så långt det går i trädet". Den tar (normalt) inte hänsyn till index och andra datastrukturer, datamängder, eller att det finns olika algoritmer för att utföra operationer som join. Det går att ha regler för det också, men då blir det så många och specialiserade regler att en kostnadsbaserad optimerare trots allt blir enklare.
En kostnadsbaserad frågeoptimerare arbetar i stället med en kostnadsfunktion, som givet en exekveringsplan räknar ut den förväntade kostnaden för att köra den. Normalt betyder "kostnad" i det här sammanhanget helt enkelt tiden det tar att köra exekveringsplanen. Kostnadsfunktionen kan ta hänsyn till olika algoritmer för att utföra en operation, till vilka index som finns, och till statistik om innehållet i databasen, till exempel om antal rader eller fördelningen av värden i en kolumn. Den kostnadsbaserade frågeoptimeraren jämför den förväntade kostnaden (enligt kostnadsfunktionen) för olika exekveringsplaner (antingen för alla som är möjliga, eller för ett urval av dem), och väljer den billigaste.
Mimer, som har en kostnadsbaserad frågeoptimerare, ger följande exekveringsplan när jag provkör:
Start of explain result
L1:
Key lookup SKOGEN.NODER, end of table goto end
compare, no hit goto L1
L2:
Index scan using index SKOGEN.FORALDER, end of table goto L1
compare, no hit goto L2
L3:
Index scan using index SKOGEN.FORALDER, end of table goto L2
compare, no hit goto L3
Record found, goto L3
end:
End of explain result
Här ser vi att den valda planen börjar med att utföra selektion på villkoret n3.nummer < 1000.
Den använder alltså ett index, som den heuristiska optimeraren inte alls bryr sig om.
Den kan också (som vi ser i uppgift 3 nedan) välja att antingen använda eller inte använda indexet,
beroende på statistik om de data som finns i tabellen, och ifall selektionsvillkoret förväntas
ha hög eller låg selektivitet.
Därefter görs två single-loop-joinar med indexering,
dvs för varje rad i delresultatet från steget innan slår den upp värdet på föräldern med hjälp av indexet
som Mimer har skapat på foralder-kolumnen.
Båda SQL-frågorna söker alltså i samma tabell, den tabellen har samma index, och i resultatet är det samma rader man vill få fram. Men ändå väljer Mimer olika exekveringsplaner, och skillnaden är om man skriver 1000 eller 1000000 i SQL-frågan. Varför väljer Mimer i det ena fallet att inte gå via indexet, trots att det finns ett index, och trots att det skulle ha blivit snabbare?
En ledtråd kan vara att provköra innan och efter att man kört kommandot update statistics. Innan man kört kommandot har Mimer inte samlat statistik om innehållet i tabellen, och bägge frågorna körs med genomläsning av hela tabellen ("sequential read"). Efter att man kört update statistics körs den andra frågan (med villkoret "mindre än en miljon") fortfarande med genomläsning av hela tabellen, men den första frågan (med villkoret "mindre än tusen") går via indexet. Mimer har alltså statistik om innehållet i databasen, och den kostnadsbaserade optimeraren använder statistiken för att ta hänsyn till vad databasen innehåller.
Mimers optimerare kan, utgående från den insamlade statistiken, sluta sig till att 1000 är ett ganska litet nodnummer, och att ganska få rader kommer att uppfylla villkoret foralder < 1000. Därför väljer den i den första frågan att gå via indexet.
Däremot verkar den insamlade statistiken inte vara tillräckligt detaljerad för att inse att nodnumren är "snett" fördelade, med mycket få mellan ett och en miljon, och nästan alla mellan en miljon och två miljoner. Därför inser optimeraren inte att även villkoret foralder < 1000000 kommer att ge ganska få rader.
I det här fallet vill först transaktion A läsa noden med nummer 19 med select-kommandot, och den begär då, och får, ett läslås.
I steg 2 vill även transaktion B läsa samma data, och även den begär, och får, ett läslås. Därefter vill transaktion B ändra noden, och den begär ett skrivlås. Men eftersom transaktion A har ett läslås, kan B inte få ett skrivlås, så den får vänta innan den kan köra sitt update-kommando.
I steg 3 vill transaktion A ändra noden, och den begär ett skrivlås. Men eftersom transaktion B har ett läslås, kan A inte få ett skrivlås, så den får vänta innan den kan köra sitt update-kommando.
Nu väntar transaktionerna på varandra, ingen kan köra vidare, och deadlock har uppstått.
Det händer ibland, och databashanterare som arbetar med lås kontrollerar därför om deadlock uppstår. Om deadlock har uppstått måste en av transaktionerna avbrytas, och dess ändringar rullas tillbaka. I det här fallet har inga ändringar gjorts i databasen.
Man kan tycka att det vore praktiskt om de här transaktionerna, som ju ska ändra i data, kunde begära skrivlås redan från början, så slipper man deadlock. Men det fungerar normalt inte så, för det en normal databashanterare ser är bara att det kommer ett select-kommando, och den kan inte veta att det senare kommer att komma ett update-kommando. Tänk på hur det fungerar i JDBC eller när man sitter och skriver SQL för hand i Batch SQL eller DB Visualizer. Användaren begär inga lås, utan databashanteraren sköter det automatiskt, baserat på vilka kommandon den ser att transaktionen vill utföra.
(Men: konservativ tvåfaslåsning går ut just på att transaktionen skaffar alla lås redan vid starten.)
Svar som säger något om att när en av transaktionerna ska committa så uppstår en konflikt och den avbryts och rullas tillbaka är fel. Den typen av kontroll efteråt är optimistisk transaktionshantering, som i Mimer, och inte pessimistisk transaktionshantering med lås.
| Noder | |||
|---|---|---|---|
| Nummer | Foralder | VST | VET |
| 1 | null | 20 december 2013 | null |
| 2 | null | 20 december 2013 | 12 april 2014 |
| 2 | 1 | 12 april 2014 | null |
Transaktionstid anger när uppgifterna gällde i databasen, eller "vad databasen vid ett visst tillfälle trodde om verkligheten", till exempel att 24 mars 2013 la man in i databasen att en viss nod hade en viss förälder, men 8 januari 2014 ändrade man föräldern, eftersom man kommit på att den först inlagda föräldern var felaktig. (Inget hade ändrats ute i verkligheten, utan det var bara en ändring i databasen.) I en relationsdatabas utan inbyggt stöd för tidsdimensionen transaktionstid kan man lägga till två kolumner, ofta kallade TST (Transaction Start Time) och TET (Transaction End Time):
| Noder | |||
|---|---|---|---|
| Nummer | Foralder | TST | TET |
| 4711 | 17 | 24 mars 2013 | 8 januari 2014 |
| 4711 | 18 | 8 januari 2014 | null |
Med transaktionstid tas aldrig några data bort fysiskt ur databasen, utan alla gamla felaktiga uppgifter finns kvar, men markerade som att de inte längre gäller.
Man kan kombinera de två dimensionerna, och i en relationsdatabas utan inbyggt stöd för tidsdimensioner får man fyra extra tidskolumner:
| Noder | |||||
|---|---|---|---|---|---|
| Nummer | Foralder | VST | VET | TST | TET |
| 1 | null | 20 december 2013 | null | 20 december 2013 | null |
| 2 | null | 20 december 2013 | null | 21 december 2013 | 12 april 2014 |
| 2 | null | 20 december 2013 | 12 april 2014 | 12 april 2014 | null |
| 2 | 1 | 12 april 2014 | null | 12 april 2014 | null |
Tidsdimensionerna hjälper inte på annat sätt än att det finns kvar en historik över trädets utseende och databasens innehåll. Om man behöver den historiken, till exempel för att man vill kunna rulla tillbaka felaktiga ändringar, har man förstås nytta av att den finns. Annars inte.
Och ja, det blir problem med integritetsvillkor:
Hade det varit bättre eller sämre att lagra skogen i form av en objektorienterad eller objektrelationell databas, i stället för en vanlig relationsdatabas?
Här är det meningen att man ska resonera om de olika alternativen på ett sätt som visar att man förstått skillnaderna mellan dem. Både "ja" och "nej" kan vara godkända svar, beroende på motiveringarna.
Själv skulle jag svara "nej". Det är enkla frågor och ett enkelt schema, och vi har ingen omedelbar nytta av något stöd för objektorientering, så varför inte använda enkel och beprövad teknik.
b)
Hade det varit bättre eller sämre att inte alls lagra skogen med hjälp en databashanterare, utan bara med vanliga datastrukturer i ett språk som C eller Java?
Det kan vara bättre. Det kan bli en mycket snabbare lösning, och (beroende på hur van programmerare man är) kanske också enklare att göra. Å andra sidan får man inte de fördelar med transaktioner, säkerhet och ändringar i såväl data som schema som en databas ger.
Här är två implementationer av ett program som läser in hela skogen (i exemplet drygt en miljon noder) till en hashtabell:
Minnesåtgången för en miljon noder är ungefär 40 megabyte. Det är förstås inte något problem för dagens datorer, som har flera gigabyte primärminne.
Å andra sidan finns det inget stöd i den här lösningen för att ändra data, olika användare med olika rättigheter, eller samtidig åtkomst vid ändringar.
c) Skogen växer från en miljon (106) till en biljon (1012) noder. Ändras svaret i delfråga b? Motivera svaret!
Det är fortfarande inte orimligt, men nu blir det mycket krångligare.
Nu blir minnesåtgången ungefär en miljon gånger större, dvs ungefär 40 terabyte. Det är flera tusen gånger mer minne än vad en normal persondator har idag, och även mycket mer än stora serverdatorer. Vi kan inte längre läsa in alla noderna i primärminnet, utan vi måste hitta en annan lösning. (Även textfilen som skulle läsas in vid programstarten blir stor, ungefär 30 terabyte, och det är mer disk än vad som finns i en normal persondator.) Vi behöver göra en diskbaserad lösning, där datat finns på disk, och programmet söker direkt i datat på disken. Det är inte orimligt, och det går att göra, men är lite krångligare än programmet ovan. Vi behöver förstås också en dator med mer disk än vanligt. När jag skriver detta rymmer de största hårddiskarna som finns på prisjakt.nu bara 6 terabyte, så vi behöver åtminstone sju sådana hårddiskar för att lagra datat.
Å andra sidan är databaser inte magiska, och även en diskbaserad databas kommer att behöva stora mängder disk för att få plats med databasen. Vanliga relationsdatabaser är gjorda för att hantera stora datamängder, men nu är det så mycket data att det inte är självklart att det fungerar. Man måste kontrollera att både databashanteraren och det underliggande operativsystemet klarar så stora datamängder, och ens valda datatyper (vanliga 32-bitars heltal räcker inte längre till för nodnumret), och filsystemet på disken, och förstås att det finns tillräckligt med diskar, och att alla diskarna går att koppla in i datorn. (Och det blir inte roligt att ta backup.)
Kanske ska man titta på en distribuerad databas, och kanske NoSQL?
En viktig del i svaret på delfråga b och c är att man ska förstå datamängder, och kunna göra enkla beräkningar. Går mina data in i minnet? Får de plats på disken? Och om de inte får plats på disken om jag lagrar dem i en fil, kommer de att få plats bara för att jag lägger dem i en databas?