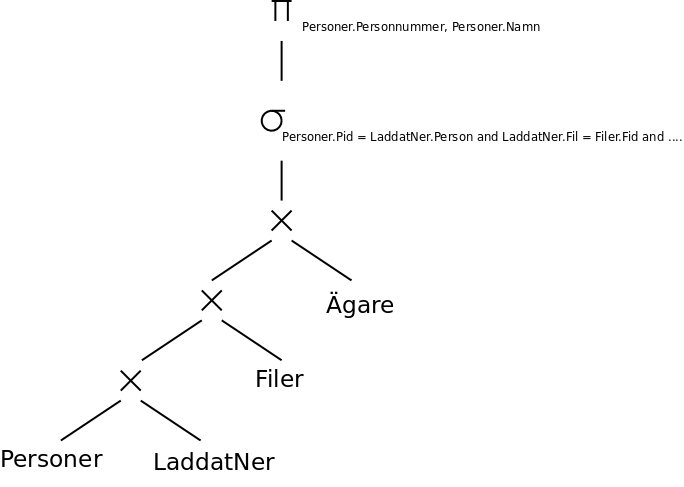
I uttrycket nedan ska PROJECT egentligen vara grekiska bokstaven lilla pi, SELECT ska egentligen vara grekiska bokstaven lilla sigma, och X ska vara ett kryss. I många specifikationer av relationsalgebra tillåter man heller inte kvalificerade namn som Personer.Personnummer, utan bara enkla namn som Personnummer.
PROJECTPersoner.Personnummer, Personer.Namn(SELECTPersoner.Pid = LaddatNer.Person and LaddatNer.Fil = Filer.Fid and Filer.Ägare = Ägare.Äid and Ägare.Namn = "Sony Music" and LaddatNer.Datum = "2009-04-04"(Personer X LaddatNer X Filer X Ägare)
b) (1p)

c) (4p)
Optimeraren utgår från den ooptimerade relationsalgebrarepresentationen av frågan, i deluppgift a och b ovan. Vi delar först upp villkoret i selektionsoperationen i flera, för att senare kunna flytta runt dem:
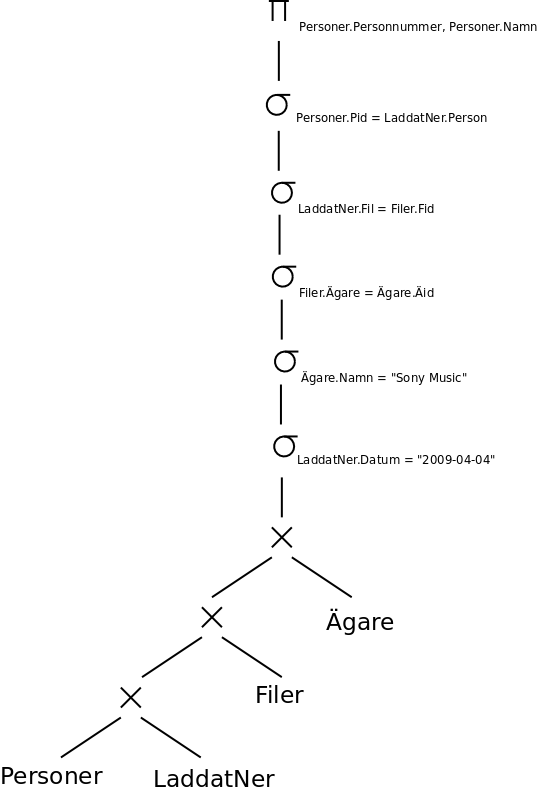
Vi trycker ner varje selektionsoperation så långt det går i trädet:
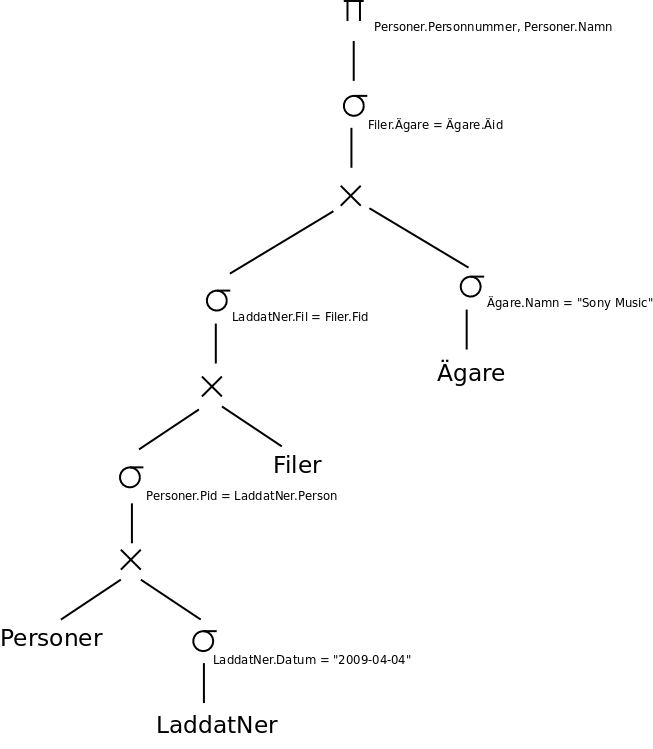
Där det går kombinerar vi en kartesisk produkt följd av en selektion till en join:
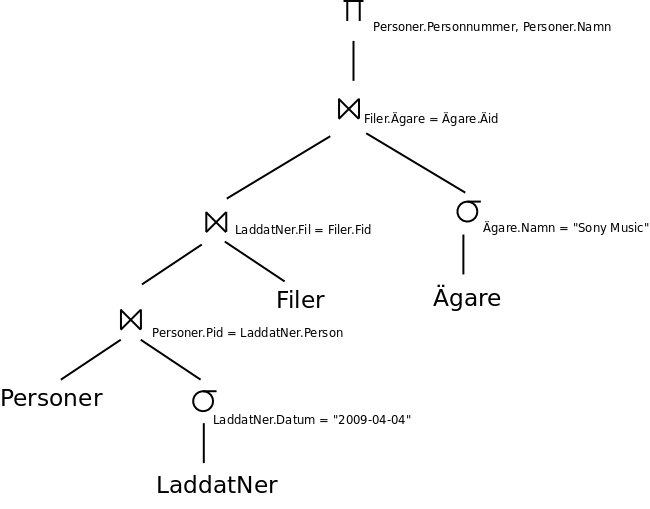
Vi trycker ner projektioner så långt det går i trädet:
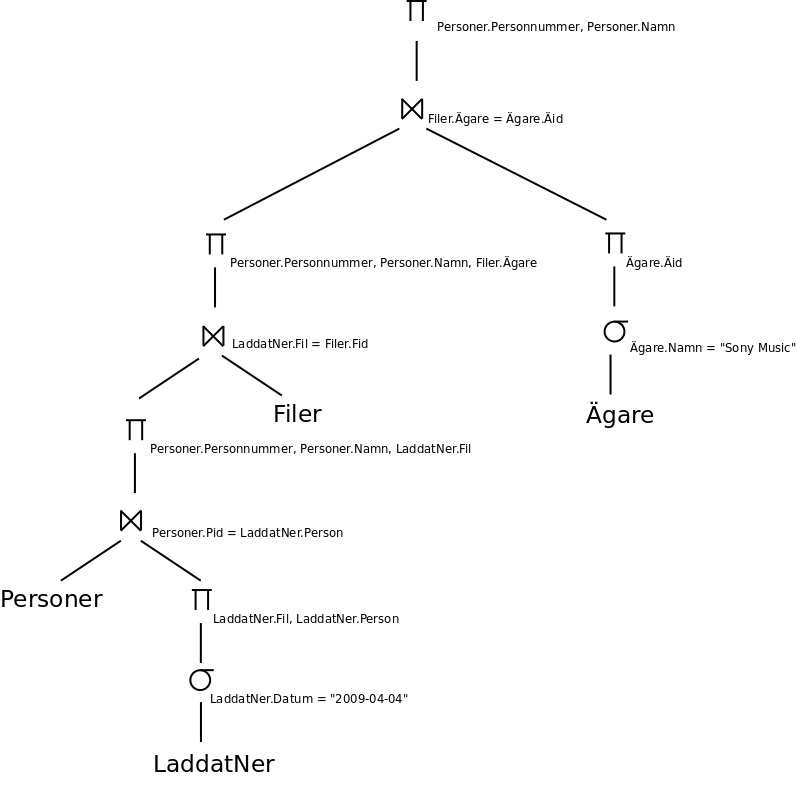
Vi gör inte projektioner direkt på tabellerna Personer och Ägare, för dessa projektioner skulle innebära att vi går igenom tabellerna en extra gång.
Om den ursprungliga frågan formulerats med tabellerna i en annan ordning, hade vi kanske också behövt ändra ordningen på de kartesiska produkterna, för att senare kunna slå samman kartesiska produkter och selektioner till joinar.
Man kan också vilja utföra den mest restriktiva selektionen först. Om optimeraren vet att Ägare.Namn är en nyckel, kan det vara bra att göra selektionen på detta attribut före den på LaddatNer.Datum, och det kan också påverka join-ordningen.
d) (1p)
En kostnadsbaserad frågeoptimerare har en kostnadsfunktion, som givet en exekveringsplan räknar ut den förväntade kostnaden för att köra den. Normalt betyder "kostnad" i det här sammanhanget helt enkelt tiden det tar att köra exekveringsplanen. Kostnadsfunktionen kan ta hänsyn till olika algoritmer för att utföra en operation, till vilka index som finns, och till statistik om innehållet i databasen. Den kostnadsbaserade frågeoptimeraren jämför den förväntade kostnaden (enligt kostnadsfunktionen) för olika exekveringsplaner (antingen för alla som är möjliga, eller för ett urval av dem), och väljer den billigaste.
e) (2p)
Till skillnad från (normal) heuristisk optimerare kan en kostnadsbaserad optimerare ta hänsyn till index och andra lagringsstrukturer, till antal rader och annan statistik om innehållet i databasen, och till olika algoritmer för att utföra operationer som join och selektion.
Vi har ingen nytta av indexet på Pid, utan måste läsa tabellen sekvensiellt. Vi antar att Personnummer är en nyckel, och deklarerad så i databasen, och att det därför i genomsnitt räcker med att läsa hälften av raderna i tabellen.
Vi antar att Pid är 4 byte, Personnummer är 13 byte och Namn 40 byte. En rad är då 57 byte. Med en blockstorlek på 2048 byte får vi en blockningsfaktor på 2048 / 57, avrundat nedåt, dvs 35. Tabellens data upptar då 107 / 35, dvs 285714 block.
Vi antar att det tar 1 ms att läsa ett block i sekvens. Då tar det i genomsnitt 285714 * 1 / 2 = 142857 ms = 143 s, dvs drygt två minuter,
(Detta är förmodligen pessimistiskt räknat. En modern hårddisk är snabbare än så vid sekvensiell läsning.)
b) (2p)
Vi antar att en blockpekare är 4 byte, och Personnummer är fortfarande 13 byte. Ett indexblock är 2048 byte, och trädet har därför ordningen (2048 - 4) / (13 + 4) + 1, avrundat nedåt, dvs 121. I ett B-träd som byggts upp dynamiskt är noderna i genomsnitt 2/3 fulla. Den effektiva fanouten i detta B+-träd är alltså 121 * 2/3, dvs ca 81.
Eftersom det är ett sekundärindex krävs det en datablockspekare från den lägsta indexnivån per datapost. Den lägsta indexnivån innehåller därför 107 / 81 = 123457 indexblock. Indexnivå 2 innehåller 123457 / 81 = 1524 indexblock. Indexnivå 3 innehåller 1524 / 81 = 18 indexblock. Indexnivå 4 består av ett enda indexblock, rotblocket.
En uppslagning på personnummer via indexet kräver fem blockläsningar (fyra indexblock och ett datablock). Om vi antar att det tar i genomsnitt 10 ms att läsa ett godtyckligt block, kommer frågan att i genomsnitt ta 50 ms att köra.
c) (2p)
Eftersom en enda sökning, med indexet i b-frågan, tar 50 ms, skulle hundra sökningar ta 5000 ms, dvs 5 sekunder. Med denna lagringsstruktur, och utan parallellism och cachning, går det inte att göra flera hundra sådana sökningar per sekund.
Man kan tänka sig flera sätt att förbättra prestandan, vilket kan göra att databasen klarar sin tänkta uppgift. Exempel:
Om vi antar att läsoperationer inte sparas i loggfilen:
T1 startar T2 startar T3 startar T1 skriver X, gamla värdet, nya värdet T1 committad T2 skriver Y, gamla värdet, nya värdet T2 skriver Z, gamla värdet, nya värdet |
b) (3p)
Nej, tidsschemat är inte serialiserbart. Man kan se det på hur T2 och T3 arbetar med Z:
| Tid | T1 | T2 | T3 |
|---|---|---|---|
| 4 | Läs(Z) | ||
| 7 | Läs(Z) | ||
| 12 | Skriv(Z) | ||
| 14 | Skriv(Z) |
Det värde på Z som T3 skriver baseras på det gamla värdet som T3 läste. Men det värdet gäller inte längre när T3 skriver, eftersom T2 hunnit skriva över det. Antag till exempel att båda transaktionerna ökar Z med ett. I ett seriellt schema, där transaktionerna körs efter varandra, blir slutresultatet förstås att Z ökas med två. Med detta schema ökas Z bara med ett, eftersom T3 skriver över T2:s ändring.
Man kan också uttrycka det så här:
Betrakta de två paren av motstridiga (se b-frågan nedan) operationer 7-12 och 12-14. Om transaktionerna körs seriellt med T2 först, kommer 7-12 i omvänd ordning. Om transaktionerna körs seriellt med T3 först, kommer 12-14 i omvänd ordning. Alltså finns inget seriellt tidsschema som är konfliktekvivalent med det givna tidsschemat.
b) (1p)
Serialiserbarhet för ett tidsschema, dvs att tidsschemat ska vara serialiserbart, innebär att tidsschema är ekvivalent med något seriellt tidsschema. Ett seriellt tidsschema är ett tidsschema där transaktionerna utförs efter varandra, utan någon överlappning i tiden.
Med ekvivalens menar man oftast konfliktekvivalens, vilket innebär att alla motstridiga ("conflicting") operationer i två transaktioner måste komma i samma ordning. Två operationer är motstridiga om de tillhör olika transaktioner och arbetar med samma dataobjekt i databasen, och minst en av dem är en skrivoperation.
Konfliktekvivalens garanterar även resultatekvivalens. Resultatekvivalens innebär att databasens innehåll, givet ett visst startinnehåll i databasen, är detsamma efter tidsschemat.
c) (5p)
Tvåfaslåsning med enkla binära lås. Vi antar att vi använder strikt tvåfaslåsning: objekten låses när de behövs första gången, och låsen släpps först vid commit.
| Tid | T1 | T2 | T3 |
|---|---|---|---|
| 1 | Start | ||
| 2 | Start | ||
| Lås(Y) | |||
| 3 | Läs(Y) | ||
| Lås(Z) | |||
| 4 | Läs(Z) | ||
| Lås(X) | |||
| 5 | Läs(X) | ||
| 6 | Start | ||
| Lås(Z)... | |||
| 9 | Skriv(X) | ||
| 10 | Commit | ||
| LåsUpp(X) | |||
| 11 | Skriv(Y) | ||
| 12 | Skriv(Z) | ||
| 13 | Commit | ||
| LåsUpp(Y) | |||
| LåsUpp(Z) | |||
| ...Lås(Z) | |||
| 7 | Läs(Z) | ||
| Lås(Y) | |||
| 8 | Läs(Y) | ||
| 14 | Skriv(Z) | ||
| 15 | Commit | ||
| LåsUpp(Y) | |||
| LåsUpp(Z) |
Tvåfaslåsning med läs- och skrivlås. Vi antar att vi använder strikt tvåfaslåsning: objekten låses när de behövs första gången, och låsen släpps först vid commit.
| Tid | T1 | T2 | T3 |
|---|---|---|---|
| 1 | Start | ||
| 2 | Start | ||
| LäsLås(Y) | |||
| 3 | Läs(Y) | ||
| LäsLås(Z) | |||
| 4 | Läs(Z) | ||
| LäsLås(X) | |||
| 5 | Läs(X) | ||
| 6 | Start | ||
| LäsLås(Z) | |||
| 7 | Läs(Z) | ||
| LäsLås(Y) | |||
| 8 | Läs(Y) | ||
| SkrivLås(X) | |||
| 9 | Skriv(X) | ||
| 10 | Commit | ||
| LåsUpp(X) | |||
| SkrivLås(Y)... | |||
| SkrivLås(Z)... |
Deadlock! Antingen T2 eller T3 måste avbrytas och rullas tillbaka.
En samling data som är avsedd för analytiska frågor, dvs frågor som försöker hitta samband och trender. Eftersom den används för analys snarare än den dagliga driften, kan den vara organiserad på ett annat sätt än en vanlig driftsdatabas. Exempelvis används ofta andra datamodeller än relationsmodellen. Den innehåller ofta mer data än de vanliga driftsdatabaserna, dels eftersom den kan innehålla data som sammanställts från flera driftsdatabaser, men också eftersom den kan innehålla historiska (dvs gamla) data. Dess data ändras kanske också mer sällan än i en vanlig databas, exempelvis genom att data importeras från driftsdatabaserna en gång i månaden. (Se boken för detaljer och exempel.)
b) (2p)
En faktatabell och flera dimensionstabeller. Faktatabellen innehåller referensattribut som refererar till dimensionstabeller, så att det bildas en "stjärna" med faktatabellen i mitten. Används när man lagrar en datakub i form av relationer i en relationsdatabas. (Se boken för detaljer och exempel.)
c) (2p)
En tabell som innehåller de olika värden som kan förekomma längs en av dimensionerna i datakuben. Används när man lagrar en datakub i form av relationer i en relationsdatabas. (Se boken för detaljer och exempel.)