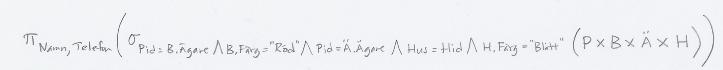
a) (4p)
Ange en stor fördel med var och en av dessa, jämfört med de andra.
b) (2p)
Om du personligen skulle skriva ett tillämpningsprogram som arbetar mot databasen i scenariot ovan, vilken av dessa tekniker skulle du välja? Utgå från din egen tillgång till verktyg, och egna kunskaper inom programmeringsspråk med mera. Motivera varför du valde just den tekniken.
a) (2p)
Vad är skillnaden mellan giltighetstid och transaktionstid? Förklara, med tabellen Personer från scenariot som exempel.
b) (1p)
De flesta databashanteraren har inget inbyggt stöd för tidsdimensioner, utan om man behöver hantera tidsdimensioner måste man göra det i form av vanliga tabeller (om det nu är en relationsdatabas). Hur skulle man implementera giltighetstid i Personer-tabellen?
c) (1p)
Hur skulle man implementera transaktionstid i Personer-tabellen?
d) (2p)
Visa med exempel från scenariodatabasen vilka problem med referensintegritet som man kan få, när man lägger till tidsdimensioner.
| Tid | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| 1 | Start | |||
| 2 | Läs(X) | |||
| 3 | Skriv(X) | |||
| 4 | Commit | |||
| 5 | Start | |||
| 6 | Start | |||
| 7 | Start | |||
| 8 | Läs(X) | |||
| 9 | Läs(Y) | |||
| 10 | Läs(Z) | |||
| 11 | Läs(X) | |||
| 12 | Läs(Y) | |||
| 13 | Skriv(X) | |||
| 14 | Skriv(Y) | |||
| 15 | Commit | |||
| 16 | Commit | |||
| 17 | Skriv(Z) | |||
| 18 | Commit |
a) (2p)
Här användes ingen metod för att hålla transaktionerna isolerade från varandra. Vilket eller vilka fel kan ha uppstått i databasen på grund av detta?
b) (4p)
Välj någon av metoderna för isolering av transaktioner, förklara kort hur metoden fungerar, och visa hur tidsschemat ovan skulle förändras om den metoden användes.
Gör rimliga antaganden om blockstorlek mm, och räkna ut hur lång tid det i genomsnitt tar att köra denna fråga, om tabellen är lagrad:select Namn, Adress from Personer where Pid = 4711;
a) utan något index (eller annan sökväg) på Pid
b) med ett primärindex i form av ett B+-träd på Pid
c) med ett sekundärindex i form av ett B+-träd på Pid
Här är en SQL-fråga som tar fram namn och adress på de personer som Thomas Padron-McCarthy:
Med samma antaganden om blockstorlek mm som ovan, hur lång tid tar det i genomsnitt att köra denna fråga, om tabellen är lagrad:select Namn, Adress from Personer where Namn = 'Thomas Padron-McCarthy';
d) utan något index (eller annan sökväg) på Namn
e) med ett sekundärindex i form av ett B+-träd på Namn
Ange antagandena, och visa hur du räknat!
a) (1p)
b) (1p)
c) (4p)
Vi börjar med att dela upp selektionen i flera, och "trycker ner" varje del så långt det går i frågeträdet:
Vi gör om varje kartesisk produkt som följs av en (lämplig) selektion, till en join:
För att slippa onödiga kolumner i delresultaten kan man lägga in projektioner. Här låter vi varje selektion och join följas av en sådan projektion, eftersom vi ändå går igenom alla raderna då. Däremot lägger vi inte in några projektioner direkt på de ursprungliga tabellerna, för arbetet med att gå igenom alla raderna och göra en extra operation är förmodligen mer än vad vi tjänar på att ha färre kolumner (men lika många rader) i de direkt efterföljande operationerna.
a) (2p)
b) (1p)
c) (3p)
Vilka saker finns i det optimerade uttrycket som en kostnadsbaserad frågeoptimerare (eller en heuristisk optimerare som bryr sig om datamängder och lagringsstrukturer) skulle kunna gjort bättre? (Alternativt, ifall det redan råkat bli helt perfekt, vad kunde den heuristiska optimeraren ha missat?)
a) (1p)
hur ett fragementeringsschema kan se ut
b) (1p)
hur rekonstruktionsprogrammet (även kallat återskapandeprogrammet) ser ut, givet fragementeringsschemat ovan
c) (2p)
hur en global fråga kan lokaliseras genom att globala relationer ersätts med med sina rekonstruktionsprogram
d) (2p)
hur detta relationsalgebrauttryck kan förenklas genom att man reducerar bort tomma deluttryck
| Observera: Välj ut och besvara (högst) sju av åtta uppgifterna. (Skulle du svara på alla åtta, räknas den med högst poäng bort.) |