Databasteknik II: Lösningar till tentamen 2008-03-29

Uppgift 1 (6 p)

Några fördelar med ODBC:
ODBC kommer från Microsoft men är en öppen standard och finns för många operativsystem och alla (för lämpliga värden på "alla") relationsdatabashanterare. Har funnits länge, och är väl etablerat. Lätt att byta server, och typ av databashanterare, i ett klientprogram.

Några fördelar med ESQL:
SQL-koden är mer integrerad med C-programmet, jämfört med andra tekniker. (Man skriver SQL-koden mitt bland den vanliga C-koden, men markerad med orden EXEC SQL, och man kan relativt enkelt komma åt C-variabler från SQL-koden.) Mer nybörjarvänligt (dvs lättare att komma igång med) än åtminstone ODBC.

Några fördelar med JDBC:
Java, så mer lättprogrammerat än ODBC och ESQL. Plattformsoberoende (så länge det finns en Java-maskin). Objektorienterat. Någorlunda enkelt att byta server, och typ av databashanterare, i ett klientprogram.

Några fördelar med ADO.NET:
Det finns bra stöd, med färdiga klasser och programmeringsverktyg, i Visual Studio. ADO.NET kan också användas för att lagra data som lokala XML-filer, på ungefär samma sätt som med databaser. Objektorienterat.

b) (2p)

Här finns det inget enda rätt svar, utan meningen är att man ska visa att man har så god koll på teknikerna att man kan relatera dem till sin egen situation.

Om jag (Thomas) själv skulle programmera, beror det mycket på vilket system och vilket språk som tillämpningsprogrammet skrivs i. Om det var ett Java-program, skulle jag välja JDBC, eftersom jag redan kan det någorlunda bra, och eftersom JDBC enklast med Java. Om det var C eller C++, skulle jag välja ODBC, eftersom jag kan det någorlunda bra och det finns ODBC-drivrutiner till nästan alla databashanterare. Även olika scriptspråk, som på ett enkelt sätt erbjuder åtkomst av databaser, brukar kunna göra detta via en ODBC-drivrutin.

Uppgift 2 (6 p)

Giltighetstid handlar om att man lagrar i databasen när data gäller, och gällde, ute i verkligheten. Transaktionstid handlar om att man lagrar i databasen när data gäller, och gällde, i databasen, dvs vad "databasen trodde" om verkligheten vid olika tidpunkter.

I en snapshot-databas, dvs en vanlig databas som beskriver världen vid en viss tidpunkt, finns bara en rad per person, och den beskriver var den personen bor just nu. (Eller egentligen: var databasen tror att den personen bor just nu.)

I en tabell med giltighetstid kan det finnas flera olika versioner av en viss persons rad, som beskriver var den personen bott vid olika tidpunkter. Till exempel kanske Zeke bodde på Gatan 4 innan han flyttade till sin nuvarande adress, Vägen 3. I så fall finns det två versioner av Zekes rad: en som gällde tidigare, och en som gäller nu.

I en tabell med transaktionstid kan det finnas flera olika versioner av en viss persons rad, för vi sparar alltid alla gamla versioner om vi gör ändringar eller borttagningar. Om vi till exempel stavade fel till Zeke, så behåller vi den gamla, felstavade versionen av raden, associerad med en notering om när den gällde, och lägger in en ny separat radversion med det rättade namnet.

b) (1p)

Varje logisk rad kan förekomma i flera olika radversioner, med de olika data som gällt vid olika tillfällen i tiden. Man lägger till två kolumner, som anger när den radens data började respektive slutade gälla ("Valid Start Time" och "Valid End Time").

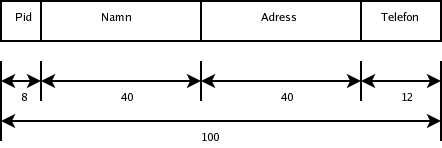
Personer med giltighetstid

Förklaringar:

• 1997 flyttade Zeke till Vägen 3, och fick telefonnummer 174590. Han har bott där, och haft det telefonnumret, ända sen dess. Null-värdet i VET-kolumnen betyder att raden fortfarande gäller.
• 2002 flyttade Zarah till Vägen 5, och hon bodde där till 2004. 2004 flyttade hon till Gränden 11, och hon har bott där sen dess. Hon hade till en början ingen telefon, men 2006 skaffade hon en telefon med nummer 260088.
• Zubeide bodde på Sörgården från 1979 till 2007, då hon flyttade till Vägen 3. Kanske flyttade hon ihop med Zeke?
• Zlatan bodde på Stigen 8 under nästan hela 2004, men vi har ingen uppgift om var han bott därefter. Zlatan är inte med i den aktuella snapshot-tabellen.

c) (1p)

Varje logisk rad kan förekomma i flera olika radversioner, med de olika data som funnits i databasen vid olika tillfällen i tiden. Man lägger till två kolumner, som anger när den radens data las in respektive togs bort (eller ändrades) ur databasen ("Transaction Start Time" och "Transaction End Time"). Rader i denna temporala tabell kan aldrig tas bort eller ändras, förutom att TET-fältet kan ändras från null till aktuellt klockslag för att ange att raden övergått från att vara den aktuella radversionen till att vara en historisk radversion.

Personer med transaktionstid

Förklaringar:

• Vi la in Zeke i databasen 19 mars, men stavade fel, och ändrade strax därefter till rätt stavning. Null-värdet i TET-kolumnen betyder att raden är den aktuella radversionen.
• Vi la in Zarah i databasen 20 mars, och har inte gjort några ändringar av hennes data sen dess.
• Vi la in Zubeide i databasen 24 mars, och strök henne ur databasen 27 mars. Vi la in henne på nytt, med samma adress och telefonnummer, 3 april. Mellan 27 mars och 3 april fanns Zubeide inte med i snapshot-tabellen.

d) (2p)

I tabellen Bilar ser vi till exempel att bil nummer 1, en röd Renault, ägs av person nummer 3, Zubeide. Referensintegritet mellan kolumnen Ägare och tabellen Personer innebär att om det står att en viss person, som nummer 1, äger en bil, så ska det också finnas en person nummer 1 i den refererade tabellen.

I en temporal databas kan en logisk rad, till exempel "Zubeides rad", finnas i flera olika versioner, som gäller för olika tidsintervall antingen i verkligheten (giltighetstid) eller i databasen (transaktionstid). Därför måste man ta hänsyn till dessa tidsintervall, och inte bara till värdena på referensattribut och refererade nycklar.

Här är ett exempel. Vi tänker oss att båda tabellerna Bilar och Personer har giltighetstid. Här är raderna för bil 1 och person 3 från de tabellerna:

Tabellen Bilar

Personer med giltighetstid

Här ser vi att bil nummer 1 köptes (eller erhölls som present) 1967 av person nummer 17. 1978 överläts den (kanske som julklapp?) till person nummer 3, Zubeide. Men det fanns (enligt vad som står i databasen) ingen Zubeide förrän 1979!

Vanlig referensintegritet i snapshot-databaser (dvs databaser utan tidsdimensioner) måste kontrolleras vid insättning, borttagning och ändring av rader. Det gäller även i en temporal databas.

Uppgift 3 (6 p)

Inga problem kan ha uppstått med transaktion T1 (som är tidsmässigt separerad från alla de andra) eller med transaktion T4 (som är datamässigt separerad från alla de andra). Men det kan ha blivit problem mellan transaktion T2 och T3. Transaktion T2 läser X och Y, och skriver X. Transaktion T3 läser X och Y, och skriver sedan Y, men vid skrivningen av Y har X ändrats. Om Y:s nya värde baseras på det gamla X, kan vi få en inkonsistens i databasen, eftersom X nu har ett nytt värde.

Exempel:

Låt X pch Y vara bankkonton som innehåller 1000 respektive 100 kronor. Transaktion T2 beräknar 10 procents ränta på Y, och adderar den till X. Transaktion T3 beräknar 10 procents ränta på X, och adderar den till Y. Om transaktionerna körs seriellt i ordningen T2-T3, blir slutresultatet att X innehåller 1010 kronor, och Y 201 kronor. Om transaktionerna körs seriellt i ordningen T3-T2, blir slutresultatet att X innehåller 1020 kronor, och Y 200 kronor. Med tidsschemat i uppgiften, blir slutresultatet att X innehåller 1010 kronor, och Y 200 kronor. Det resultatet kan man inte få med något seriellt schema, och eftersom definitionen på "korrekt tidsschema" är att det ska vara ekvivalent med något seriellt tidsschema, är tidsschemat i uppgiften fel.

b) (4p)

Binära lås

Vi visar först grundläggande tvåfaslåsning med binära lås. Binära lås innebär att varje transaktion måste låsa varje dataobjekt som den vill läsa eller skriva, och senare låsa upp det. Ett dataobjekt kan endast vara låst av en transaktion åt gången. Om dataobjektet redan är låst när en transaktion vill låsa det, får transaktionen stå still och vänta tills objektet blir upplåst igen.

Tvåfaslåsning innebär att när en transaktion låst upp något dataobjekt, får den inte låsa några fler objekt.

Läs- och skrivlås

Här är grundläggande eller strikt tvåfaslåsning (de ser likadana ut i början) med läs- och skrivlås, och uppgradering från läs- till skrivlås. Med läs- och skrivlås kan flera transaktioner samtidigt ha läslås på samma dataobjekt, men skrivlås måste vara exklusiva. Endast transaktion T2 och T3 visas här.

Tidsstämplar

Med tidsstämpelmetoden, som den beskrivs i boken, sker rollback av transaktion T2 i steg 13, eftersom man ser på läs-tidsstämpeln för X att X redan har lästs av den "framtida" transaktionenen T3. T2 kan inte skriva dit ett nytt värde, för då skulle det ju vara detta nya värde som T3 borde ha läst.

Uppgift 4 (6 p)

Vi antar att en datapost är 100 bytes:

Vi antar också att datablock är 2 kilobyte (2048 bytes), vilket innebär att blockningsfaktorn (antalet poster som ryms i ett block) är 2048/100 = 20. Det betyder att det krävs 1000000 / 20 = 50000 datablock.

Vi måste läsa datafilen sekvensiellt. Vi antar att det tar i genomsnitt 1 millisekund att läsa ett datablock när man läser blocken i sekvens. I genomsnitt hittar vi rätt post efter halva filen. Det tar alltså i genomsnitt 50000 * 0.001 / 2 = 25 sekunder att köra frågan.

(1ms per block på 2 kilobyte är mycket pessimistiskt räknat, med moderna diskar. Som ett maximalt optimistiskt alternativ till 1ms/block kan man i stället räkna på överföringshastigheten från disken. Antag en överföringshastighet på 3.0 Gbit/s, som är teoretiskt max för SATA. Då tar det 10⁶*100*8/(3*10⁹)/2 = 0.13 sekunder. Men det är som sagt maximalt optimistiskt räknat.)

b) med ett primärindex i form av ett B⁺-träd på Pid

Vi antar att även indexblocken är 2 kilobyte (2048 bytes).

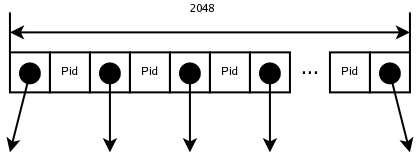
Om vi antar att Pid (som i deluppgift a ovan) är 8 byte, och att även en blockpekare är 8, blir B⁺-trädets ordning (2048 - 8) / (8 + 8) + 1 = 128. Eftersom noder i ett B-träd som byggs upp dynamiskt bara är i genomsnitt 2/3 fulla, räknar vi med en effektiv ordning på 2/3 * 128 = 85.

Om B⁺-trädsindexet används för att lägga in dataposterna i datablocken, och att datablocken delas när de blir fulla, blir även datablocken i genomsnitt 2/3 fulla. Då blir den effektiva blockningsfaktorn 2/3*20 = 13. Alltså behövs 10000000/13 = 76923 datablock.

I ett primärindex behövs en indexpost (i den lägsta indexnivån) per datablock, alltså 76923 stycken. På den lägsta indexnivån behövs därför 76293 / 85 = 898 indexblock. På indexnivå 2 behövs 898 / 85 = 11 indexblock. Ytterligare en nivå behövs för rotblocket.

Alltså behövs fyra blockläsningar (tre indexblock plus ett datablock). Vi antar att det tar i genomsnitt 5 millisekunder att läsa ett godtyckligt datablock. Det tar alltså i genomsnitt 4 * 0.005 = 0.020 sekunder att köra frågan.

c) med ett sekundärindex i form av ett B⁺-träd på Pid

I ett sekundärindex är indexet inte ordnat i samma ordning som datafilen, så där behövs en indexpost (i den lägsta indexnivån) per datapost, alltså 1000000 stycken. På den lägsta indexnivån behövs därför 1000000 / 85 = 11764 indexblock. På indexnivå 2 behövs 11764 / 85 = 138 indexblock. På indexnivå 3 behövs 138 / 85 = 2 indexblock. Ytterligare en nivå behövs för rotblocket.

Alltså behövs fem blockläsningar (fyra indexblock plus ett datablock). Vi antar att det tar i genomsnitt 5 millisekunder att läsa ett godtyckligt datablock. Det tar alltså i genomsnitt 5 * 0.005 = 0.025 sekunder att köra frågan.

d) utan något index (eller annan sökväg) på Namn

Namn är förmodligen inte en nyckel, så vi måste alltid läsa hela datafilen. Om vi räknar med fulla datablock, som i deluppgift a (men inte b), finns det 50000 datablock, och det tar i genomsnitt 50000 * 0.001 = 50 sekunder att köra frågan.

e) med ett sekundärindex i form av ett B⁺-träd på Namn

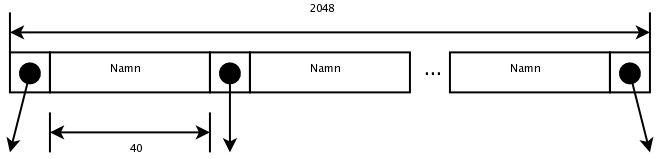
Namn är 40 byte, en blockpekare är 8 byte, och ett indexblock är 2048 byte. B⁺-trädets ordning blir (2048 - 8) / (40 + 8) + 1 = 43. Vi räknar med en effektiv ordning på 2/3 * 43 = 29.

I ett sekundärindex behövs en indexpost (i den lägsta indexnivån) per datapost, alltså 1000000 stycken. På den lägsta indexnivån behövs därför 1000000 / 29 = 34483 indexblock. På indexnivå 2 behövs 34483 / 29 = 1189 indexblock. På indexnivå 3 behövs 1189 / 29 = 41 indexblock. På indexnivå 4 behövs 41 / 29 = 2 indexblock. Ytterligare en nivå behövs för rotblocket.

Alltså behövs sex blockläsningar (fem indexblock plus ett datablock). Vi antar att det inte är så många som har det namnet, för annars hade man behövt läsa flera datablock. Det tar (fortfarande) i genomsnitt 5 millisekunder att läsa ett godtyckligt datablock. Det tar alltså i genomsnitt 6 * 0.005 = 0.030 sekunder att köra frågan.

Uppgift 5 (6 p)

Klicka på bilderna för att se dem i större format.

a) (1p)

b) (1p)

Notera att vanliga operatorer, som "+", "-" och kartesisk produkt, är vänsterassociativa, så PxBxÄxH betyder ((PxB)xÄ)xH, inte till exempel (PxB)x(ÄxH).

c) (4p)

Vi börjar med att dela upp selektionen i flera, och "trycker ner" varje del så långt det går i frågeträdet:

Vi gör om varje kartesisk produkt som följs av en (lämplig) selektion, till en join:

För att slippa onödiga kolumner i delresultaten kan man lägga in projektioner. Här låter vi varje selektion och join följas av en sådan projektion, eftersom vi ändå går igenom alla raderna då. Däremot lägger vi inte in några projektioner direkt på de ursprungliga tabellerna, för arbetet med att gå igenom alla raderna och göra en extra operation är förmodligen mer än vad vi tjänar på att ha färre kolumner (men lika många rader) i de direkt efterföljande operationerna.

Nu stod tabellerna i den ursprungliga SQL-frågan redan i en lämplig ordning för att joinas ihop i det optimerade relationsalgebrauttrycket. Annars hade man också behövt ta hänsyn till de olika möjliga joinordningarna.

Uppgift 6 (6 p)

a) (2p) Vi skriver in antalet rader i tabellerna och de olika delresultaten:

Antalet rader i resultatet av selektionen måste vi gissa, men sannolikt är den selektionens selektivitet (dvs hur stor del av raderna som den "släpper igenom") ganska låg, så det kommer att vara mycket färre än 10²⁶ rader som sen ska behandlas i projektionen. Därför spelar det inte så stor roll exakt hur många rader som skickas till projektionen, för det kommer att vara den sista kartesiska produkten och selektionen som helt dominerar exekveringstiden.

Vill man vara noggrannare i sin uppskattning kan man räkna så här:

• Det finns en miljon bilar, och en miljon personer, så i genomsnitt äger varje person en bil. Låt oss anta att det finns tio olika färger. Om färger och ägande är jämnt fördelat, kommer en av tio personer (dvs hundra tusen) att äga en röd bil.
• Det finns hundra tusen hus. Med samma tio olika färger, och jämn fördelning av färgerna, finns det tio tusen blå hus.
• Det finns en miljon personer, och en miljon "husäganden", så (om vi fortfarande antar jämn fördelning) kommer varje hus att ägas gemensamt av tio personer, och varje person är med och äger ett hus. Av miljonen personer, kommer en av tio (dvs hundra tusen) att vara med och äga ett blått hus.
• Om de olika ägandena och färgerna är oberoende, är det en chans på hundra att en person äger både en röd bil och ett blått hus. Det betyder att 10000 personer kommer med i svaret.

Hur lång tid tar då detta att köra? Vi ignorerar alla operationer utom den sista kartesiska produkten och selektionen, för dessa två hanterar hundra tusen gånger fler rader än någon av de andra operationerna. Om vi alltså antar att den sista kartesiska produkten och selektionen hanterar 10²³ rader vardera, är det totalt 2*10²³ rader som ska hanteras. Datorn hanterar 10¹³ rader per sekund. Det tar alltså 2*10²³/10¹³ sekunder, dvs 2*10¹⁰ (20 miljarder) sekunder, att köra frågan, vilket motsvarar 2*10¹⁰/3600/24/365.25 = 712 år.

b) (1p)

Även här skriver vi in antalet rader i tabellerna och de olika delresultaten. Som i a-uppgiften måste vi gissa selektiviteter, och vi antar även här att det finns tio olika, jämnt fördelade färger.

Hur många rader "hanterar" en join som joinar ihop två mellanresultat med radantalen A och B? Det beror på joinalgoritmen, men vi antar nested-loop-join, vilket betyder A gånger B. Så exempelvis den första joinen, som joinar ihop 10⁶ och 10⁵ rader, antas hantera 10¹¹ rader.

Vi summerar alla operationernas radantal:

• Två selektioner: 10⁶ + 10⁶
• Tre joinar: 10¹¹ + 10¹¹ + 10¹⁰
• Fem projektioner: 10⁵ + 10⁵ + 10⁵ + 10⁵ + 10⁴

c) (3p)

Till skillnad från (normal) heuristisk optimerare kan en kostnadsbaserad optimerare ta hänsyn till olika algoritmer för att utföra operationer som join, till vilka index som finns, och till statistik om innehållet i databasen.

• Den kostnadsbaserade optimeraren kan välja mellan olika join-algoritmer. Om det till exempel finns ett index på Personer.Pid (vilket verkar troligt), kan den första joinen göras som single-loop-join i stället för nested-loop-join, och då blir den sådär en halv miljon gånger snabbare.
• Den kostnadsbaserade optimeraren tar hänsyn till datamängder. Om det till exempel finns en miljon bilar och bara tio hus, borde vi kanske börja med husen (och de få personer som äger ett blått hus) i stället för bilarna (och de många personer som äger en röd bil).
• Den kostnadsbaserade optimeraren kan ta hänsyn till fördelningen av data. Kanske finns det tusen olika färger på hus, men bara tio olika färger på bilar, vilket ger att selektionen på husfärg förmodligen blir mer selektiv än den på bilfärg, och därför borde den göras först.

Uppgift 7 (6 p)

Nested-loop-join:

I den yttre loopen går man igenom alla raderna i den ena tabellen. För varje sådan rad går man, i en inre loop, igenom alla raderna i den andra tabellen. För varje kombination av rader (dvs, i den inre loopens kropp) beräknar man joinvillkoret, och om det ger ett sant värde, tas den radkombinationen med i svaret.

Single-loop-join, även kallad indexerad nested-loop-join:

I den yttre loopen går man igenom alla raderna i den ena tabellen. För varje sådan rad gör man en uppslagning, via ett index, i den andra tabellen. (Om joinattributet i den andra kolumnen inte är en nyckel, behöver man en kort loop över de rader som har det sökta värdet.)

b) (1p) Vilken av dem är snabbast?

Single-loop-join är (normalt) snabbast.

c) (1p) Varför använder man inte alltid den, om den nu är snabbast?

• Om det inte finns något lämpligt index, kan single-loop-join inte användas.
• Om joinvillkoret inte är en likhet (som R1.A = R2.B), utan en storleksjämförelse (som R1.A < R2.B), kan nested-loop-joinen trots allt vara snabbare.
• Beroende på mängden data, och vilka värden, som finns i tabellerna, kan det variera vilken av två joinalgoritmer som ger lägst kostnad.

Uppgift 8 (6 p)

Det finns olika sorters fragmentering, och som exempel använder vi ett schema för primär horisontell fragmentering:

Personer₁ = SELECT_{Adress="Vägen 3"}(Personer)
Personer₂ = SELECT_{Adress="Gränden 11"}(Personer)
Personer₃ = SELECT_{Adress<>"Vägen 3" OCH Adress<>"Gränden 11"}(Personer)

(Jag skriver relationsalgebraoperatorerna som SELECT, PROJECT och så vidare.)

b) (1p)

Personer = Personer₁ UNION Personer₂ UNION Personer₃

c) (2p)

En global SQL-fråga:

select Namn, Telefon from Personer where Adress = "Vägen 3"

Översätt till global relationsalgebra:

PROJECT_{Namn, Telefon} ( SELECT_{Adress="Vägen 3"} ( Personer ) )

Lokaliserad relationsalgebra:

PROJECT_{Namn, Telefon} ( SELECT_{Adress="Vägen 3"} ( Personer₁ UNION Personer₂ UNION Personer₃ ) )

d) (2p)

På samma sätt som x(y+z) kan skrivas om till xy+xz, kan vi "multiplicera in" selektionen innanför unionsoperatorerna:

PROJECT_{Namn, Telefon} [ ( SELECT_{Adress="Vägen 3"} ( Personer₁ ) ) UNION ( SELECT_{Adress="Vägen 3"} ( Personer₂ ) ) UNION ( SELECT_{Adress="Vägen 3"} ( Personer₃ ) ) ]

Med hjälp av fragmenteringsschemat ser vi att dessa två deluttryck är tomma:

SELECT_{Adress="Vägen 3"} ( Personer₂ )
SELECT_{Adress="Vägen 3"} ( Personer₃ )

Vi stryker dem:

PROJECT_{Namn, Telefon} ( SELECT_{Adress="Vägen 3"} ( Personer₁ ) )