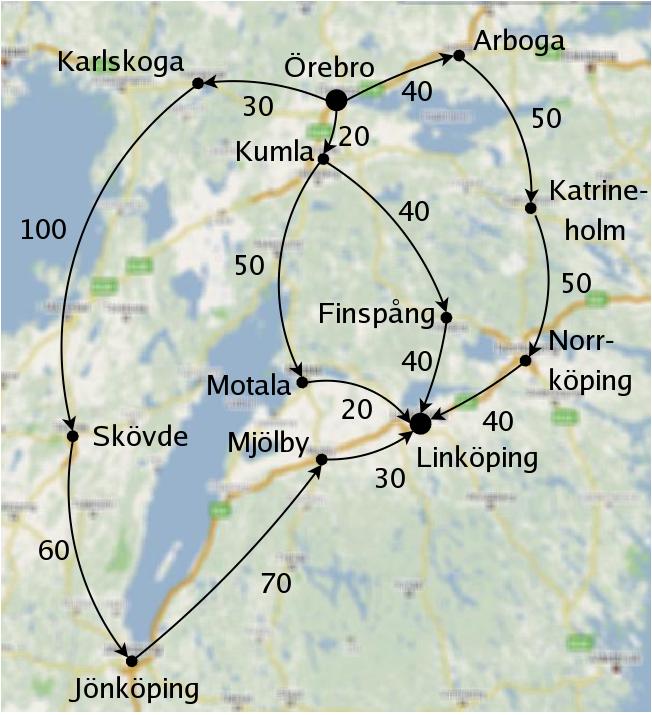

(Det är nog inte exakt samma siffror som på föreläsningen, för jag har inte de anteckningarna här.)
Som vi ser finns det fyra olika möjliga planer för hur man ska åka:
Men gör vi inte onödigt mycket jobb? Här är två förbättringar som man kanske skulle vilja göra:
Vi gör så här i stället. Börja med att skapa en "nod", som representerar utgångsplatsen Örebro. Denna nod har totalkostnaden 0, för det "kostar" 0 kilometer att åka till Örebro.

Från Örebro kan man åka tre olika vägar, så vi skapar tre nya noder för Karlskoga, Kumla och Arboga. Kostnaden för att åka från Örebro till Karlskoga är 30 kilometer, och totalkostnaden för att åka till Karlskoga blir alltså 30.
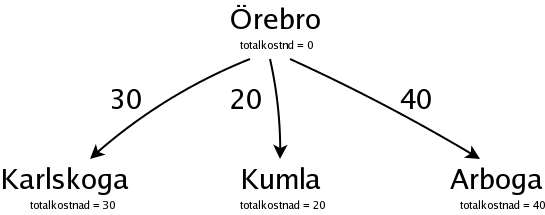
Vi kan se det som att vi har tre "partiella planer" för att åka till Linköping: Örebro -> Karlskoga, Örebro -> Kumla och Örebro -> Arboga.
Vi söker oss fram parallellt på olika möjliga vägar från Örebro, och bygger ett så kallat "sökträd". Men vi ska inte bygga ett fullständigt träd, som innehåller alla vägar, utan vi fortsätter hela tiden på den väg som verkar mest lovande, vilket betyder den som (än så länge) är billigast. I det här fallet är det Kumla, för Kumla har den lägsta totalkostnaden. Från Kumla kan man åka till Motala eller till Finspång, så vi gör två nya noder för Motala och Finspång:
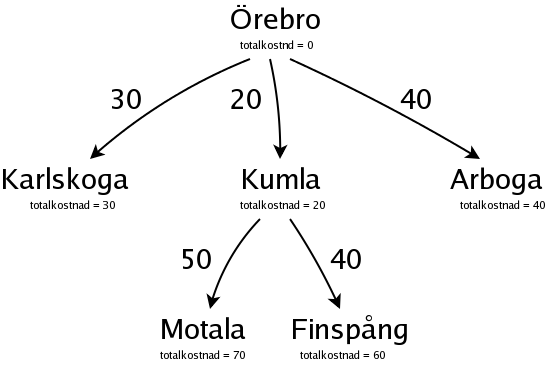
Nu är det Karlskoga, med totalkostnaden 30, som är billigast, och därför mest lovande. Från Karlskoga kan man åka till Skövde:
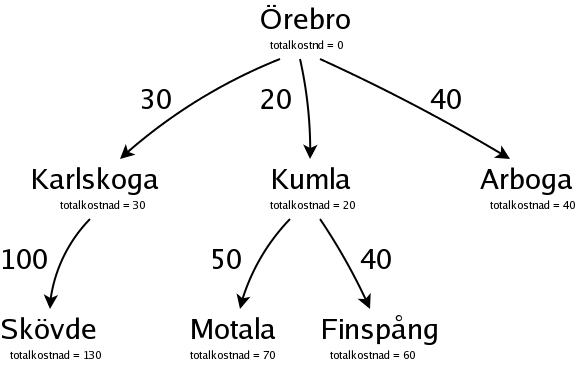
Nu är det Arboga, med totalkostnaden 40, som är billigast, och därför mest lovande. Från Arboga kan man åka till Katrineholm:
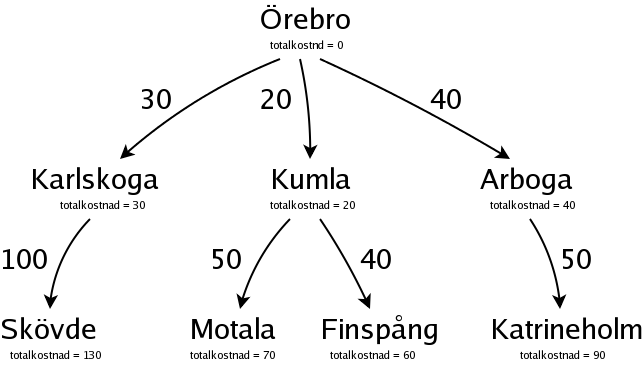
Nu är det Finspång, med totalkostnaden 60, som är billigast, och därför mest lovande. Från Finspång kan man åka till Linköping:
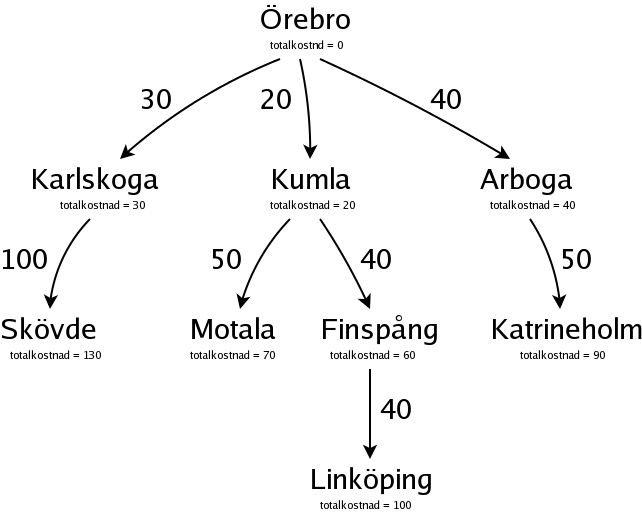
Vi har alltså hittat en komplett plan, med kostnaden 100, för att åka till Linköping. Men vi är inte klara än. Noderna för Motala och Katrineholm har båda en totalkostnad som är lägre än 100, och det kan ju hända att den kompletta vägen till Linköping via någon av dessa blir lägre än 100. Vägen via Skövde är däremot omöjlig, för redan i Skövde är totalkostnaden 130.
Därför fortsätter vi, som vanligt med den mest lovande noden, och det är Motala, med totalkostnaden 70.
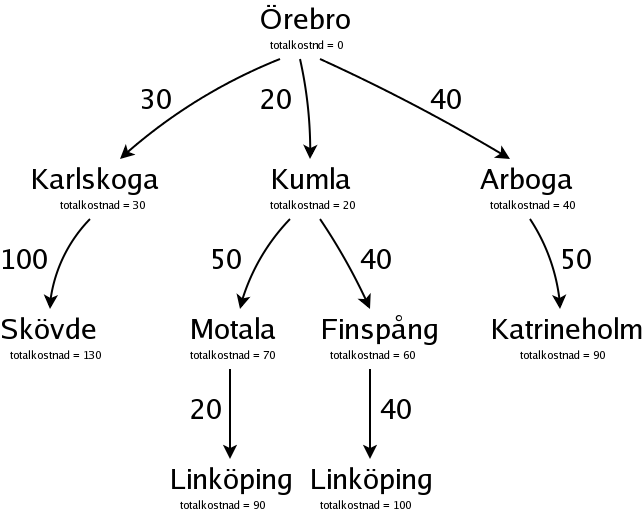
Nu hittade vi en ny komplett plan, med kostnaden 90, och det är den nya billigaste planen.
Dessutom ser vi att ingen annan väg kan bli billigare, och alltså är det planen Örebro -> Kumla -> Motala -> Linköping, med kostnaden 90, som är den billigaste planen.
Sammanfattning:
Dynamisk programmering bygger upp ett sökträd genom att hela tiden bygga vidare på den mest lovande vägen. Till skillnad från "riktig" fullständig sökning behöver vi inte titta på precis alla möjliga väger, för vi skippar dem som vi vet är sämre. Till skillnad från slumpmässiga metoder, som på ett eller annat sätt väljer bort en del vägar baserat på slump eller gissningar, är vi med dynamisk programmering garanterade att alltid hitta den bästa vägen, för vi skippar ju bara dem som vi verkligen vet är sämre.
Frågeoptimeraren i AMOS jobbar ju inte med vägar, utan med listor av predikat, som ska sorteras i en viss ordning, så de bildar en exekveringsplan. (Läs mer om exekveringsplaner i AMOS.) Om man har tre predikat, låt oss kalla dem X, Y och Z, som ska sorteras, så får vi börja med en nod som representerar en tom partiell plan:

Denna tomma partiella plan har kostnaden noll, och vi räknar med fanout 1.
Vi har tre predikat att välja mellan, och planen kan börja med något av dem:
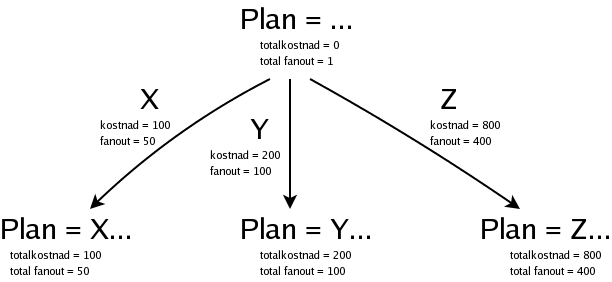
Nu har vi alltså tre partiella planer, och vi väljer att bygga vidare på den billigaste av dem, nämligen planen som börjar med X och som har kostnaden 100:
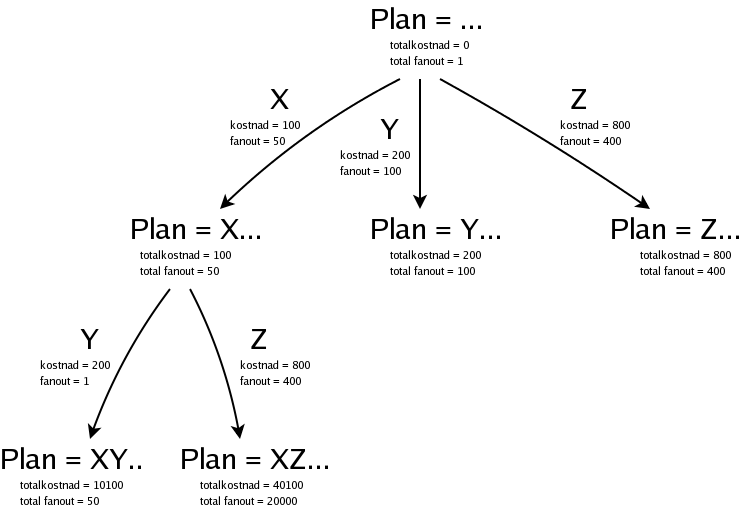
Det är lite krångligare att räkna ut totalkostnaden för en (partiell) planen, för eftersom predikaten i exekveringsplanen körs som nästlade loopar kan vi inte bara addera kostnaden för de olika predikaten, utan vi måste ta hänsyn till antalet varv som loopen ska köras, det som vi kallar fanout. Läs mer i beskrivningen av exekveringsplaner i AMOS.
Notera att vi inte alltid kan använda alla predikaten på alla platser i planen. Ta till exempel villkoret _v1 > 100000. Om vi började med den, först i planen, så har _v1 ännu inte något värde, så det är inte bara att kolla om villkoret stämer. I stället kommer exekveringsplanen att innehålla en loop som går igenom alla de heltal som villkoret stämmer för, och det blir ju ganska många heltal. (2147583647 stycken, om man räknar med trettiotvåbitarstal. Betydligt fler om man räknar med riktiga, matematiska heltal.) Funktionen simple-pred-cost, som returnerar kostnaden och fanouten för ett predikat, kommer då att returnera nil.