Programmering grundkurs och Programmering C
för D1 m fl, även distanskursen
lördag 26 februari 2011
Gäller som tentamen för:
DT1016 Datateknik A, Programmering grundkurs, provkod 0100
DT1007 Datateknik A, Tillämpad datavetenskap, provkod 0410
DT1006 Datateknik A, Programmering C, distans, provkod 0100
| Hjälpmedel: | Inga hjälpmedel. |
| Poängkrav: |
Maximal poäng är 40.
För godkänt betyg (3 respektive G) krävs 20 poäng. |
| Resultat och lösningar: | Meddelas via e-post eller på kursens hemsida, http://basen.oru.se/kurser/c/2010-2011-p2/, senast lördag 19 mars 2011. |
| Återlämning av tentor: | Efter att resultatet meddelats kan tentorna hämtas på universitetets centrala tentamensutlämning. |
| Examinator och jourhavande: | Thomas Padron-McCarthy, telefon 070-73 47 013. |
| Prioritet | Kategori | Operator | Associativitet |
|---|---|---|---|
| Högsta | Unära postfixoperatorer | (), [], ->, ., ++, -- | vänster |
| Unära prefixoperatorer | !, ++, --, +, -, *, &, sizeof, (typ) | höger | |
| Multiplikation mm | *, /, % | vänster | |
| Addition mm | +, - | vänster | |
| Jämförelser | <, <=, >=, > | vänster | |
| Likhetsjämförelser | ==, != | vänster | |
| Logiskt OCH | && | vänster | |
| Logiskt ELLER | || | vänster | |
| Lägsta | Tilldelning | =, +=, -=, *=, /=, %= | höger |

Om man vet längden på kateterna a och b i en rätvinklig triangel, kan man använda Pythagoras sats för att beräkna längden på hypotenusan h:
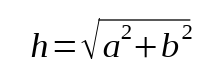
Skriv ett fullständigt C-program (med #include och allt) som läser in kateterna a och b, och sen skriver ut hypotenusan h.
Ett körexempel, med användarens inmatning kursiverad:
Ange a: 8 Ange b: 3.14 h = 8.594161
|
I den här och alla andra uppgifter på tentan gäller:
Normalt är felhantering en stor del av ett program. Vad ska till exempel hända om användaren skriver Kalle när hon egentligen borde mata in ett tal? Här behövs dock ingen felhantering, om så inte särskilt efterfrågas i uppgiften. |
a = 1; b = a + 2; c = 3; d = 4;
while (a < b) {
if (b == c && b == d) {
a = a / 2 + 1 * 2;
++b;
}
else {
a = a / 2 + 1 * 3;
b--;
}
}
Ett körexempel, med användarens inmatning kursiverad:
Skriv ett ord: Bengt-Sofokles 14 tecken Skriv ett ord: x 1 tecken Skriv ett ord: slut Tack och hej.
Man kan anta att inget ord är längre än 317 tecken.
Skriv funktionen medel, som tar två heltal som argument, och returnerar medelvärdet av dem, men som ett flyttal. (Medelvärdet av heltalen 1 och 2 ska alltså bli 1.5.)
b)
Skriv en main-funktion som läser in två heltal, sen anropar funktionen medel för att få reda på deras medelvärde, och till sist skriver ut det medelvärdet.
|
I den här och alla andra uppgifter på tentan gäller:
Om du behöver använda något från en tidigare uppgift eller deluppgift, till exempel anropa en funktion som skrevs i den tidigare uppgiften, så behöver du inte skriva samma kod igen. Du får också göra uppgiften även om du inte gjort den tidigare uppgiften. |
Skriv funktionen mellan, som tar fyra argument: två flyttal (vi kan kalla dem min och max), en array av flyttal, och ett heltal som anger hur många flyttal som finns i den arrayen. Funktionen ska returnera ett heltal som anger hur många av talen i arrayen som ligger mellan de två talen min och max.
b)
Skriv en main-funktion som först läser in tusen flyttal till en array, sen anropar funktionen mellan för att få reda på hur många av dessa tal som ligger mellan 3 och 3.5, och till sist skriver ut det antalet.
Skapa datatypen struct Tal, som ska användas för att representera ett tal med felgränser. Denna post ska innehålla tre flyttal: det uppskattade värdet, och sen min- och max-gränsen för talets verkliga värde.
100.000000 (min: 82.300000, max: 144.300000)
Du får själv välja vilket av dessa två funktionshuvuden du ska använda:
struct Tal las_tal() void las_tal(struct Tal *p)
När man jämför två tal som har felgränser kan det bli lite komplicerat. Om man inte vet säkert hur stora talen är, kan man inte alltid veta vilket som är störst.
Exempelvis vet vi att ett tal med min-gränsen 3 och max-gränsen 4 är mindre än ett tal med min-gränsen 5 och max-gränsen 6. Men om vi jämför ett tal med min-gränsen 3 och max-gränsen 5, och ett tal med min-gränsen 4 och max-gränsen 6, kan vi inte veta vilket som egentligen är störst.
Skriv funktionen storre, som tar två tal-poster som argument, och som returnerar 1 om det första talet är större än det andra, 0 om det första talet är mindre än eller lika med det andra, och -1 om det inte går att avgöra.